
Six rods of the same mass m and length $l$are arranged as shown in figure. Calculate the coordinate of the centre of mass of the system
A. $(\dfrac{l}{2},\dfrac{7l}{6})$
B. $(\dfrac{l}{3},l)$
C. $(\dfrac{l}{2},\dfrac{4l}{3})$
D. $(\dfrac{l}{2},\dfrac{5l}{3})$
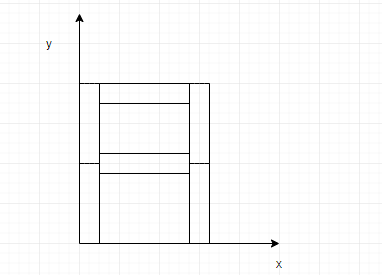

Answer
579k+ views
Hint: We’re given six rods. The centre of mass of each rod lies at the midpoint. That is if the length is $l$, it is at a distance $\dfrac{l}{2}$. Further, we have to find the coordinates of all the centre of masses, that is the centre of mass of every individual rod, as each of it contributes to the overall centre of mass of the system.
Formula used:
Centre of mass of system: \[xcm=\dfrac{\sum\limits_{i=1}^{N}{mixi}}{M}\], where m is the mass and x is the distance
Complete step by step answer:
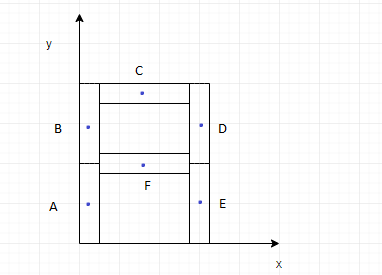
From the modified figure, we deduce that,
Coordinates of A: $(0,\dfrac{l}{2})$
Coordinates of B: $(0,\dfrac{3l}{2})$
Coordinates of C: $(\dfrac{l}{2},2l)$
Coordinates of D: $(l,\dfrac{3l}{2})$
Coordinates of E: $(l,\dfrac{l}{2})$
Coordinates of F: $(\dfrac{l}{2},l)$
Hence, we have found the coordinates of the centre of mass of each individual rod.
From the formula mentioned above,
Centre of mass of the system: \[xcm=\dfrac{mx1+mx2+mx3+mx4+mx5+mx6}{6m}\]
\[=\dfrac{x1+x2+x3+x4+x5+x6}{6}\]
Substituting the above calculated values,
$xcm=\dfrac{0+0+\dfrac{l}{2}+l+l+\dfrac{l}{2}}{6}$ $=\dfrac{3l}{6}=\dfrac{l}{2}$
Thus the value of the x coordinate is founded.
Similarly, \[ycm=\dfrac{my1+my2+my3+my4+my5+my6}{6m}\]
\[=\dfrac{y1+y2+y3+y4+y5+y6}{6}\]
Substituting the above calculated values,
\[ycm=\dfrac{\dfrac{l}{2}+\dfrac{3l}{2}+l+\dfrac{l}{2}+2l+\dfrac{3l}{2}}{6}\] $=\dfrac{7l}{6}$.
Thus, the value of the y coordinate is founded.
Hence, the centre of mass of the entire system is at $(\dfrac{l}{2},\dfrac{7l}{6})$
Note:
We can initially estimate the centre of mass by neglecting the horizontal rods.
Two parallel rods will have the centre of mass at the midpoint of the line joining their midpoints.
The contributions of the horizontal rods cause slight variation from this position.

Formula used:
Centre of mass of system: \[xcm=\dfrac{\sum\limits_{i=1}^{N}{mixi}}{M}\], where m is the mass and x is the distance
Complete step by step answer:
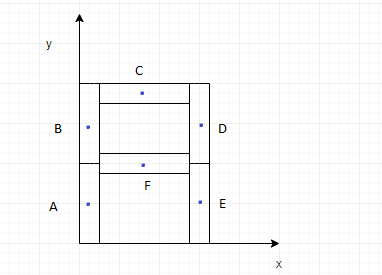
From the modified figure, we deduce that,

Coordinates of A: $(0,\dfrac{l}{2})$
Coordinates of B: $(0,\dfrac{3l}{2})$
Coordinates of C: $(\dfrac{l}{2},2l)$
Coordinates of D: $(l,\dfrac{3l}{2})$
Coordinates of E: $(l,\dfrac{l}{2})$
Coordinates of F: $(\dfrac{l}{2},l)$
Hence, we have found the coordinates of the centre of mass of each individual rod.
From the formula mentioned above,
Centre of mass of the system: \[xcm=\dfrac{mx1+mx2+mx3+mx4+mx5+mx6}{6m}\]
\[=\dfrac{x1+x2+x3+x4+x5+x6}{6}\]
Substituting the above calculated values,
$xcm=\dfrac{0+0+\dfrac{l}{2}+l+l+\dfrac{l}{2}}{6}$ $=\dfrac{3l}{6}=\dfrac{l}{2}$
Thus the value of the x coordinate is founded.
Similarly, \[ycm=\dfrac{my1+my2+my3+my4+my5+my6}{6m}\]
\[=\dfrac{y1+y2+y3+y4+y5+y6}{6}\]
Substituting the above calculated values,
\[ycm=\dfrac{\dfrac{l}{2}+\dfrac{3l}{2}+l+\dfrac{l}{2}+2l+\dfrac{3l}{2}}{6}\] $=\dfrac{7l}{6}$.
Thus, the value of the y coordinate is founded.
Hence, the centre of mass of the entire system is at $(\dfrac{l}{2},\dfrac{7l}{6})$
Note:
We can initially estimate the centre of mass by neglecting the horizontal rods.
Two parallel rods will have the centre of mass at the midpoint of the line joining their midpoints.
The contributions of the horizontal rods cause slight variation from this position.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Draw a diagram of nephron and explain its structur class 11 biology CBSE

Explain zero factorial class 11 maths CBSE

Chemical formula of Bleaching powder is A Ca2OCl2 B class 11 chemistry CBSE

Name the part of the brain responsible for the precision class 11 biology CBSE

The growth of tendril in pea plants is due to AEffect class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




