Question

What is $ \sin \theta $ and $ \cos \theta $ if $ \tan \theta = \dfrac{1}{2} $ and $ \sin \theta > 0 $ ?

Answer 1

Hint: We have to find $ \sin \theta $ and $ \cos \theta $ . Now, we know that $ \tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }} $ , so we can write $ \dfrac{{\sin \theta }}{{\cos \theta }} = \dfrac{1}{2} $ . On simplifying it we will get $ \cos \theta = 2\sin \theta $ . We know the formula $ {\sin ^2}\theta + {\cos ^2}\theta = 1 $ and we have the value for $ \cos \theta $ . So, substitute the value of $ \cos \theta $ and find the value of $ \sin \theta $ . After finding the value of $ \sin \theta $ , put it in equation $ \cos \theta = 2\sin \theta $ and you will get the value of $ \cos \theta $ as well.
Formulas used:
 $ \Rightarrow \tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }} $
 $ \Rightarrow {\sin ^2}\theta + {\cos ^2}\theta = 1 $
 $ \Rightarrow \tan = \dfrac{{{\text{Opposite}}}}{{Adjacent}} = \dfrac{1}{2} $
 $ \Rightarrow \sin \theta = \dfrac{{{\text{Opposite}}}}{{{\text{Hypotenuse}}}} $
 $ \Rightarrow \cos \theta = \dfrac{{Adjacent}}{{{\text{Hypotenuse}}}} $

Complete step-by-step answer:
In this question, we are given the value of $ \tan \theta $ and we need to find the values of $ \sin \theta $ and $ \cos \theta $ .
 $ \Rightarrow \tan \theta = \dfrac{1}{2} $ and $ \sin \theta > 0 $ - - - - - - - - - - (1)
Now, we know that $ \tan \theta $ is $ \sin \theta $ divided by $ \cos \theta $ . So, we can write equation (1) as $ \sin \theta $ divided by $ \cos \theta $ equal to $ \dfrac{1}{2} $ . Therefore, equation (1) becomes
 $ \Rightarrow \dfrac{{\sin \theta }}{{\cos \theta }} = \dfrac{1}{2} $
Cross multiply, we get
 $ \Rightarrow \cos \theta = 2\sin \theta $ - - - - - - - - - - (2)
Now, we know that the square of $ \sin \theta $ plus the square of $ \cos \theta $ is always equal to 1.
Therefore, $ {\sin ^2}\theta + {\cos ^2}\theta = 1 $ - - - - - - - - - (3)
Now, from equation (2) substitute $ \cos \theta = 2\sin \theta $ in equation (3). Therefore, we get
 $ \Rightarrow {\sin ^2}\theta + {\left( {2\sin \theta } \right)^2} = 1 $
Open the bracket, we get
 $
   \Rightarrow {\sin ^2}\theta + 4{\sin ^2}\theta = 1 \\
   \Rightarrow 5{\sin ^2}\theta = 1 \\
   \Rightarrow {\sin ^2}\theta = \dfrac{1}{5} \;
  $
Taking square root on both sides, we get
 $ \Rightarrow \sin \theta = \pm \sqrt {\dfrac{1}{5}} $
But, according to equation (1), $ \sin \theta > 0 $ . Hence, the value of $ \sin \theta $ cannot be negative.
 $ \Rightarrow \sin \theta = \sqrt {\dfrac{1}{5}} = \dfrac{1}{{\sqrt 5 }} $
Rationalizing the above equation, we get
 $ \Rightarrow \sin \theta = \dfrac{1}{{\sqrt 5 }} \times \dfrac{{\sqrt 5 }}{{\sqrt 5 }} = \dfrac{{\sqrt 5 }}{5} $
Now, from equation (2),
 $ \Rightarrow \cos \theta = 2\sin \theta $
Therefore, $ \cos \theta = 2 \times \dfrac{{\sqrt 5 }}{5} $
 $ \Rightarrow \cos \theta = \dfrac{{2\sqrt 5 }}{5} $
Hence, we have got the values of $ \sin \theta $ and $ \cos \theta $ .

Note: Alternate method to solve this question is by drawing the triangle.
We know that $ \tan = \dfrac{{{\text{Opposite}}}}{{Adjacent}} = \dfrac{1}{2} $

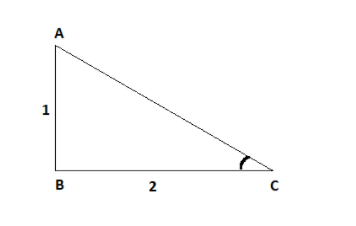
Now, in right angled triangle $ ABC $ , using Pythagoras
 $
   \Rightarrow A{B^2} + B{C^2} = A{C^2} \\
   \Rightarrow {1^2} + {2^2} = A{C^2} \\
   \Rightarrow A{C^2} = 5 \\
   \Rightarrow AC = \pm \sqrt 5 \;
  $
Now, we know that
  $
   \Rightarrow \sin \theta = \dfrac{{{\text{Opposite}}}}{{{\text{Hypotenuse}}}} = \dfrac{{AB}}{{AC}} \\
   \Rightarrow \sin \theta = \dfrac{1}{{\sqrt 5 }} \;
  $
As $ \sin \theta > 0 $ .
And, the formula for $ \cos \theta $ is
 $
   \Rightarrow \cos \theta = \dfrac{{Adjacent}}{{{\text{Hypotenuse}}}} = \dfrac{{BC}}{{AC}} \\
   \Rightarrow \cos \theta = \dfrac{2}{{\sqrt 5 }} \;
  $