Question

Simplify $ \sin \left( {{\cot }^{-1}}\left( \tan \left( {{\cos }^{-1}}x \right) \right) \right) $ .

Answer 1

Hint:
 We are given $ \sin \left( {{\cot }^{-1}}\left( \tan \left( {{\cos }^{-1}}x \right) \right) \right) $ we are asked to simplify it. To simplify we will use trigonometric ratios $ \cos \theta $ . Then we will use $ \tan \theta =\dfrac{\text{Perpendicular}}{\text{Base}} $ . After that we also require $ \tan \left( {{\tan }^{-1}}\left( \theta \right) \right)=\theta $ to simplify, after this we will follow the same step but with trigonometric ratio $ \sin \theta $ and then we use $ \sin \left( {{\sin }^{-1}}\theta \right)=\theta $ to get the final simplified answer.

Complete step by step answer:
We are given $ \sin \left( {{\cot }^{-1}}\left( \tan \left( {{\cos }^{-1}}x \right) \right) \right) $ . We are asked to find the simplified value of it.
Before we move further, we need to understand inverse trigonometry and trigonometry.
Let $ {{\cos }^{-1}}x=\theta \cdots \cdots \left( 1 \right) $ then we will get $ \cos \theta =x $ which can be written as $ \cos \theta =\dfrac{x}{1} $ .
As we know, $ \cos \theta =\dfrac{\text{Base}}{\text{Hypotenuse}} $ so considering x as base and 1 as hypotenuse.
Now as we know that $ \tan \left( {{\tan }^{-1}}\left( \theta \right) \right)=\theta $ so our equation becomes, \[\sin \left( {{\cot }^{-1}}\left( \dfrac{\sqrt{1-{{x}^{2}}}}{x} \right) \right)\left( as\text{ tan}\left( {{\tan }^{-1}}\left( \dfrac{\sqrt{1-{{x}^{2}}}}{x} \right) \right)=\dfrac{\sqrt{1-{{x}^{2}}}}{x} \right)\].
Now again consider \[\left( {{\cot }^{-1}}\left( \dfrac{\sqrt{1-{{x}^{2}}}}{x} \right) \right)=\theta \cdots \cdots \cdots \left( 3 \right)\] so we get, \[\cot \theta =\dfrac{\sqrt{1-{{x}^{2}}}}{x}\].
As \[\cot \theta =\dfrac{\text{Base}}{\text{Perpendicular}}\] so consider base as \[\sqrt{1-{{x}^{2}}}\] and perpendicular as x, so we get the triangle as

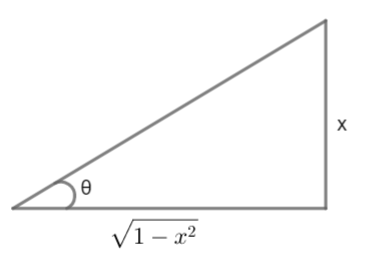
We will find value of hypotenuse using Pythagoras theorem, which says $ {{H}^{2}}={{P}^{2}}+{{B}^{2}} $ as P = x and B = \[\sqrt{1-{{x}^{2}}}\], So
\[\begin{align}
  & {{H}^{2}}={{\left( \sqrt{1-{{x}^{2}}} \right)}^{2}}+{{x}^{2}} \\
 & \Rightarrow {{H}^{2}}=1-{{x}^{2}}+{{x}^{2}} \\
 & \Rightarrow {{H}^{2}}=1 \\
\end{align}\]
Now using P = x and H = 1 we will find $ \sin \theta $ .
We construct a triangle,

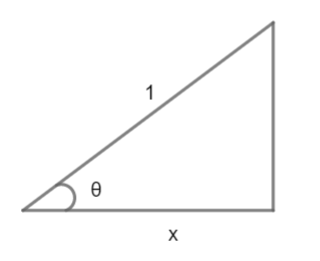
Using Pythagoras theorem which says $ {{H}^{2}}={{P}^{2}}+{{B}^{2}} $ we get, $ {{1}^{2}}={{x}^{2}}+{{P}^{2}} $ .
Now simplifying we get, $ {{1}^{2}}-{{x}^{2}}={{P}^{2}} $ .
Simplifying for P we get, $ P=\sqrt{1-{{x}^{2}}} $ .
Now using $ P=\sqrt{1-{{x}^{2}}} $ and B = x, we will find the value of $ \tan \theta $ .
As we know $ \tan \theta =\dfrac{\text{Perpendicular}}{\text{Base}} $ so $ \tan \theta =\dfrac{\sqrt{1-{{x}^{2}}}}{\text{x}} $ .
So we get the values as $ \theta ={{\tan }^{-1}}\left( \dfrac{\sqrt{1-{{x}^{2}}}}{\text{x}} \right)\cdots \cdots \cdots \left( 2 \right) $ .
Now comparing (1) and (2) we get that $ {{\cos }^{-1}}x={{\tan }^{-1}}\left( \dfrac{\sqrt{1-{{x}^{2}}}}{\text{x}} \right)\cdots \cdots \cdots \left( * \right) $ .
So our initial equation becomes $ \sin \left( {{\cot }^{-1}}\left( \tan \left( {{\cos }^{-1}}x \right) \right) \right)=\sin \left( {{\cot }^{-1}}\left( \tan \left( {{\tan }^{-1}}\left( \dfrac{\sqrt{1-{{x}^{2}}}}{\text{x}} \right) \right) \right) \right) $ using (*).
We know $ \sin \theta =\dfrac{\text{Perpendicular}}{\text{Hypotenuse}} $ so will take P = x and H = 1, so $ \sin \theta =\dfrac{\text{x}}{\text{1}} $ .
So we get the values as $ \theta ={{\sin }^{-1}}\left( \dfrac{\text{x}}{\text{1}} \right)\cdots \cdots \cdots \left( 4 \right) $ .
Now using (3) and (4) we get $ {{\sin }^{-1}}\left( \dfrac{\text{x}}{\text{1}} \right)={{\cot }^{-1}}\left( \dfrac{\sqrt{1-{{x}^{2}}}}{x} \right) $ .
So our equation becomes $ \sin \left( {{\sin }^{-1}}\left( \dfrac{\text{x}}{\text{1}} \right) \right)\left( \text{as }{{\cot }^{-1}}\left( \dfrac{\sqrt{1-{{x}^{2}}}}{x} \right)={{\sin }^{-1}}\left( \dfrac{\text{x}}{\text{1}} \right) \right) $ .
We know $ sin\left( {{\sin }^{-1}}\theta \right)=\theta $ s so we get, $ \Rightarrow \dfrac{x}{1}\left( \text{as }\sin \left( {{\sin }^{-1}}\left( \dfrac{\text{x}}{\text{1}} \right) \right)=\dfrac{x}{1} \right) $ .
Hence we get $ \sin \left( {{\cot }^{-1}}\left( \tan \left( {{\cos }^{-1}}x \right) \right) \right)=x $ .
Note:
While simplifying these types of questions, we must know about trigonometry along with inverse trigonometry. While solving, always keep track of the solution and the concept. Too many calculations are there so the focus is much needed. While using Pythagoras theorem, always remember we need the value of H or P, not their square. So root is always needed.