
Show that the sum of kinetic energy and potential energy (i.e., total mechanical energy) is always conserved in the case of a freely falling body under gravity (with air resistance neglected) from a height h by finding it when
(i) the body is at the top,
(ii) the body has fallen a distance $x$,
(iii) the body has reached the ground.
Answer
467.7k+ views
Hint: Calculate the kinetic and potential energy at each of the instances asked in the question. The sum of potential and kinetic energy gives the total mechanical energy of the system. Since we have ignored the force of friction, we don’t need to worry about the loss of energy due to friction (energy remains conserved for this system)
Formulas used:
${v^2} = {u^2} + 2as$
Where $v$ is the initial velocity, $u$ is the final velocity, $a$ is the acceleration and $s$ is the distance covered.
$U = mgh$
Where, $U$ is the total potential energy, $m$ is the mass of the object, $g$ is the acceleration due to gravity and $h$ is the height of the object from the ground
$K = \dfrac{1}{2}m{v^2}$
Where, $K$ is the total kinetic energy, $m$ is the mass of the object and $v$ is the velocity of the object at that moment.
Complete step by step answer:
So, in the given diagram a body of mass m be falling freely under gravity from a height h above the ground (i.e., from position ‘a’). Let us now calculate the sum of kinetic energy K and potential energy U at various positions, say at ‘a’ (at height h above the ground), at ‘b’ (when it has fallen through a distance x) and at ‘c’ (on the ground).
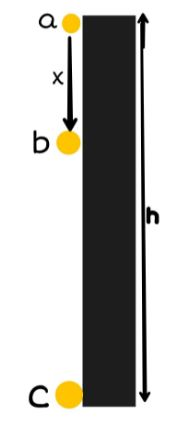
(i) At the position ‘a’ (at height h above the ground):
The initial velocity of body= 0 (since body is at rest at A)
Kinetic energy $ = \dfrac{1}{2} \times m \times {\left( 0 \right)^2} = 0$
Potential energy $U = mgh$
Hence total mechanical energy $ = 0 + mgh = mgh$...........(I)
(ii) At the position ‘b’ (when it has fallen a distance x): Let ${v_x}$ be the velocity acquired by the body at ‘b’ after falling through a distance x. Then the values initial velocity $\left( {u = 0} \right)$,distance $\left( {S = x} \right)$ and acceleration $\left( {a = g} \right)$. From the above equation ${v^2} = {u^2} + 2as$. The value of ${v_x}$ is:
${v_x}^2 = {0^2} + 2gx$ (Substituting all the values)
$\Rightarrow {v_x} = 2gx$
Hence, Kinetic energy
\[K = \dfrac{1}{2}m{v_x}^2 \\
\Rightarrow K= \dfrac{1}{2}m \times 2gx \\
\Rightarrow K = mgx\]
Now at the point ‘b’, height of body above the ground $ = h - x$.
Potential energy is,
\[U = mg\left( {h{\text{ }}-{\text{ }}x} \right)\]
The total mechanical energy is
\[T= K + U \\
\Rightarrow T = mgx + mg\left( {h{\text{ }}-{\text{ }}x} \right) \\
\Rightarrow T = mgh\].............(II)
(iii) At the position ‘c’ (on the ground): Let the velocity acquired by the body on reaching the ground be ${v_g}$. Then the values initial velocity $\left( {u = 0} \right)$, distance $\left( {S = h} \right)$ and acceleration $\left( {a = g} \right)$. From the above equation${v^2} = {u^2} + 2as$.
${v_g}^2 = {0^2} + 2gh$ (Substituting all the values)
$\Rightarrow {v_g} = 2gh$
So, kinetic energy is,
\[K = \dfrac{1}{2}m{v_g}^2 \\
\Rightarrow K= \dfrac{1}{2}m \times \left( {2gh} \right) \\
\Rightarrow K= mgh\]
Potential energy \[U = mg \times 0 = 0\] (at the ground when h = 0)
The total mechanical energy \[ = K + U = mgh + 0 = mgh\]...............(III)
It is completely clear from equation (I), (II) and (III), we get to see that the total mechanical energy which is the sum of kinetic energy and potential energy always remains constant at each point of motion and is equal to initial energy at height $h$.
Note: If friction is ignored the above is valid, but if friction is encountered the total mechanical energy decreases as the height decreases and the energy doesn’t remain conserved. In some questions the height to which the object is thrown is given to be very large (in terms comparable to the radius of earth) in such cases the value of acceleration due to gravity $\left( g \right)$ changes. In such cases we use to $\left( {U = - \dfrac{{GMm}}{X}} \right)$ calculate the potential energy of the object where $M$ is the mass of earth, $m$ is the mass of the object, $G$ is the gravitational constant and $X$ is the distance of the object from the centre of the earth.
Formulas used:
${v^2} = {u^2} + 2as$
Where $v$ is the initial velocity, $u$ is the final velocity, $a$ is the acceleration and $s$ is the distance covered.
$U = mgh$
Where, $U$ is the total potential energy, $m$ is the mass of the object, $g$ is the acceleration due to gravity and $h$ is the height of the object from the ground
$K = \dfrac{1}{2}m{v^2}$
Where, $K$ is the total kinetic energy, $m$ is the mass of the object and $v$ is the velocity of the object at that moment.
Complete step by step answer:
So, in the given diagram a body of mass m be falling freely under gravity from a height h above the ground (i.e., from position ‘a’). Let us now calculate the sum of kinetic energy K and potential energy U at various positions, say at ‘a’ (at height h above the ground), at ‘b’ (when it has fallen through a distance x) and at ‘c’ (on the ground).

(i) At the position ‘a’ (at height h above the ground):
The initial velocity of body= 0 (since body is at rest at A)
Kinetic energy $ = \dfrac{1}{2} \times m \times {\left( 0 \right)^2} = 0$
Potential energy $U = mgh$
Hence total mechanical energy $ = 0 + mgh = mgh$...........(I)
(ii) At the position ‘b’ (when it has fallen a distance x): Let ${v_x}$ be the velocity acquired by the body at ‘b’ after falling through a distance x. Then the values initial velocity $\left( {u = 0} \right)$,distance $\left( {S = x} \right)$ and acceleration $\left( {a = g} \right)$. From the above equation ${v^2} = {u^2} + 2as$. The value of ${v_x}$ is:
${v_x}^2 = {0^2} + 2gx$ (Substituting all the values)
$\Rightarrow {v_x} = 2gx$
Hence, Kinetic energy
\[K = \dfrac{1}{2}m{v_x}^2 \\
\Rightarrow K= \dfrac{1}{2}m \times 2gx \\
\Rightarrow K = mgx\]
Now at the point ‘b’, height of body above the ground $ = h - x$.
Potential energy is,
\[U = mg\left( {h{\text{ }}-{\text{ }}x} \right)\]
The total mechanical energy is
\[T= K + U \\
\Rightarrow T = mgx + mg\left( {h{\text{ }}-{\text{ }}x} \right) \\
\Rightarrow T = mgh\].............(II)
(iii) At the position ‘c’ (on the ground): Let the velocity acquired by the body on reaching the ground be ${v_g}$. Then the values initial velocity $\left( {u = 0} \right)$, distance $\left( {S = h} \right)$ and acceleration $\left( {a = g} \right)$. From the above equation${v^2} = {u^2} + 2as$.
${v_g}^2 = {0^2} + 2gh$ (Substituting all the values)
$\Rightarrow {v_g} = 2gh$
So, kinetic energy is,
\[K = \dfrac{1}{2}m{v_g}^2 \\
\Rightarrow K= \dfrac{1}{2}m \times \left( {2gh} \right) \\
\Rightarrow K= mgh\]
Potential energy \[U = mg \times 0 = 0\] (at the ground when h = 0)
The total mechanical energy \[ = K + U = mgh + 0 = mgh\]...............(III)
It is completely clear from equation (I), (II) and (III), we get to see that the total mechanical energy which is the sum of kinetic energy and potential energy always remains constant at each point of motion and is equal to initial energy at height $h$.
Note: If friction is ignored the above is valid, but if friction is encountered the total mechanical energy decreases as the height decreases and the energy doesn’t remain conserved. In some questions the height to which the object is thrown is given to be very large (in terms comparable to the radius of earth) in such cases the value of acceleration due to gravity $\left( g \right)$ changes. In such cases we use to $\left( {U = - \dfrac{{GMm}}{X}} \right)$ calculate the potential energy of the object where $M$ is the mass of earth, $m$ is the mass of the object, $G$ is the gravitational constant and $X$ is the distance of the object from the centre of the earth.
Recently Updated Pages
Why are manures considered better than fertilizers class 11 biology CBSE

Find the coordinates of the midpoint of the line segment class 11 maths CBSE

Distinguish between static friction limiting friction class 11 physics CBSE

The Chairman of the constituent Assembly was A Jawaharlal class 11 social science CBSE

The first National Commission on Labour NCL submitted class 11 social science CBSE

Number of all subshell of n + l 7 is A 4 B 5 C 6 D class 11 chemistry CBSE

Trending doubts
Differentiate between an exothermic and an endothermic class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

State the laws of reflection of light




