Question

Show that the points \[A\left( 2,3 \right)\], \[B\left( 4,5 \right)\] and $ C\left( 3,2 \right) $ can be the vertices of a rectangle. Find the coordinates of the fourth vertex?

Answer 1

Hint: We start solving the problem by finding the distances AB, BC and AC using the fact that the distance between the points $ \left( {{x}_{1}},{{y}_{1}} \right) $ and $ \left( {{x}_{2}},{{y}_{2}} \right) $ is $ \sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}} $ . We then consider $ A{{B}^{2}}+A{{C}^{2}} $ and check whether it is equal to $ B{{C}^{2}} $ as we know that any three points in a rectangle can together form a right angle-angles triangle. We then assume the fourth vertex and then use the property that the midpoint of two diagonals in the rectangle is same to find the required coordinates of fourth vertex.

Complete step by step answer:
According to the problem, we need to prove that the points \[A\left( 2,3 \right)\], \[B\left( 4,5 \right)\] and $ C\left( 3,2 \right) $ can be the vertices of a rectangle. We then need to find the coordinates of the fourth vertex.
Let us find the distances AB, BC, and AC.
We know that the distance between the points $ \left( {{x}_{1}},{{y}_{1}} \right) $ and $ \left( {{x}_{2}},{{y}_{2}} \right) $ is $ \sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}} $ .
Now, let us find the distance AB.
 $ \Rightarrow AB=\sqrt{{{\left( 4-2 \right)}^{2}}+{{\left( 5-3 \right)}^{2}}} $ .
 $ \Rightarrow AB=\sqrt{{{\left( 2 \right)}^{2}}+{{\left( 2 \right)}^{2}}} $ .
 $ \Rightarrow AB=\sqrt{4+4} $ .
 $ \Rightarrow AB=\sqrt{8} $ ---(1).
Now, let us find the distance BC.
 $ \Rightarrow BC=\sqrt{{{\left( 3-4 \right)}^{2}}+{{\left( 2-5 \right)}^{2}}} $ .
 $ \Rightarrow BC=\sqrt{{{\left( -1 \right)}^{2}}+{{\left( -3 \right)}^{2}}} $ .
 $ \Rightarrow BC=\sqrt{1+9} $ .
 $ \Rightarrow BC=\sqrt{10} $ ---(2).
Now, let us find the distance AC.
 $ \Rightarrow AC=\sqrt{{{\left( 3-2 \right)}^{2}}+{{\left( 2-3 \right)}^{2}}} $ .
 $ \Rightarrow AC=\sqrt{{{\left( 1 \right)}^{2}}+{{\left( -1 \right)}^{2}}} $ .
 $ \Rightarrow AC=\sqrt{1+1} $ .
 $ \Rightarrow AC=\sqrt{2} $ ---(3).
Let us consider $ A{{B}^{2}}+A{{C}^{2}} $ . From equations (1) and (3), we get
 $ \Rightarrow A{{B}^{2}}+A{{C}^{2}}={{\left( \sqrt{8} \right)}^{2}}+{{\left( \sqrt{2} \right)}^{2}} $ .
 $ \Rightarrow A{{B}^{2}}+A{{C}^{2}}=8+2 $ .
 $ \Rightarrow A{{B}^{2}}+A{{C}^{2}}=10 $ .
 $ \Rightarrow A{{B}^{2}}+A{{C}^{2}}={{\left( \sqrt{10} \right)}^{2}} $ .
From equation (2), we get $ A{{B}^{2}}+A{{C}^{2}}=B{{C}^{2}} $ .
We can see that the points ABC can form a right-angled triangle with a right angle at vertex A. We know that any three points in a rectangle can together form a right angle-angle triangle.
Let us assume the fourth vertex be $ D\left( a,b \right) $ .
Now, let us draw the figure to represent all the obtained information.

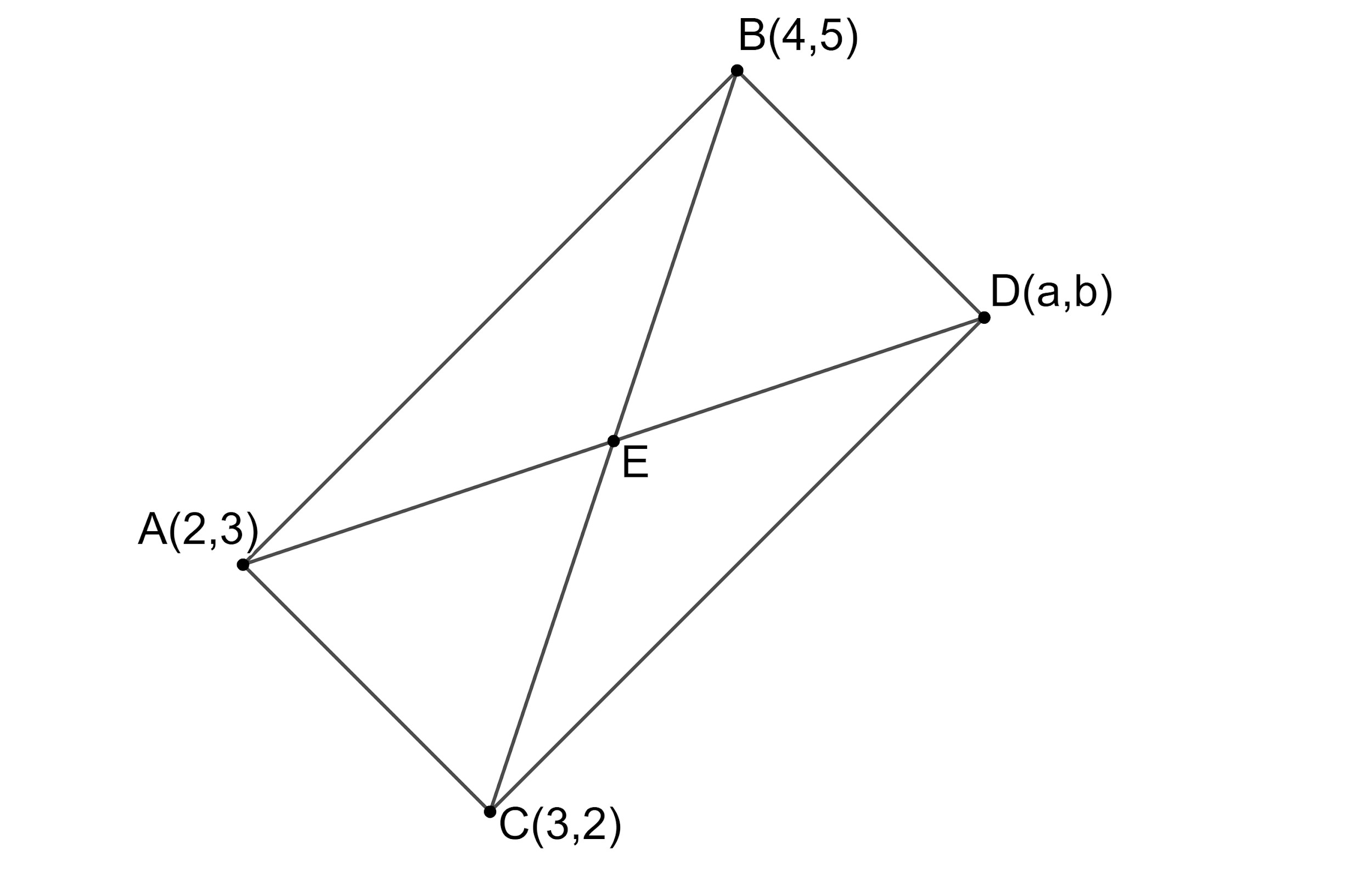
We know that the mid-point of both the diagonals AD and BC is the same i.e., point E.
We know that the mid-point of the points $ \left( {{x}_{1}},{{y}_{1}} \right) $ and $ \left( {{x}_{2}},{{y}_{2}} \right) $ is $ \left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right) $ .
So, we get $ \left( \dfrac{2+a}{2},\dfrac{3+b}{2} \right)=\left( \dfrac{3+4}{2},\dfrac{5+2}{2} \right) $ .
 $ \Rightarrow \left( \dfrac{2+a}{2},\dfrac{3+b}{2} \right)=\left( \dfrac{7}{2},\dfrac{7}{2} \right) $
 $ \Rightarrow \dfrac{2+a}{2}=\dfrac{7}{2} $ , $ \dfrac{3+b}{2}=\dfrac{7}{2} $ .
 $ \Rightarrow 2+a=7 $ , $ 3+b=7 $ .
 $ \Rightarrow a=5 $ , $ b=4 $ .
So, we have found the coordinates of the fourth vertex of the rectangle as $ \left( 5,4 \right) $.
 $ \therefore $ The fourth vertex of the rectangle is $ \left( 5,4 \right) $ .

Note:
 We can see that the given problem contains a huge amount of calculation, so we need to perform each step carefully in order to avoid confusion and calculation mistakes. We can also verify points A, B, C as the vertices of the rectangle by finding the slope of the segments AB and AC and then making use of the fact that the product of the slopes of perpendicular lines is –1. We can also find the fourth vertex by finding the intersection of lines perpendicular to sides AC and AB which were passing through C and B.