Question

Show that the function $h\left( x \right)=\tan x$ is differentiable at any $a\in \mathbb{R}$ and $a$ is not an odd multiple of $\dfrac{\pi }{2}$ and $h'\left( a \right)={{\sec }^{2}}a$. In general, if $x$ is not an odd multiple of $\dfrac{\pi }{2}$, then $h'\left( x \right)={{\sec }^{2}}x.$.

Answer 1

Hint: To check the differentiability of a function, we will find the derivative of the function. To find the derivative $h'\left( x \right)$ of the function $h\left( x \right)$, we can use the first principle of derivative and the functional relations given in the question.

Complete step-by-step answer:
 In the question, it is given a function; \[h\left( x \right)=\tan x\]
To check differentiability of this function, we have to find the derivative of $h\left( x \right)$. To find the derivative of the given function, we will use the first principle of derivative from which, the derivative of any function is given by the formula;
$\Rightarrow f'\left( x \right)=\underset{h\to 0}{\mathop{\lim }}\,\dfrac{f\left( x+h \right)-f\left( x \right)}{h}$
In the question, the function is $h\left( x \right)=\tan x$. Substituting $h\left( x \right)=\tan x$and $h\left( x+h \right)=\tan (x+h)$, we get;
\[\Rightarrow h'\left( x \right)=\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\left( \tan \left( x+h \right)-\tan x \right)}{h}\]
We have a formula in trigonometry; \[\tan \left( x+h \right)=\dfrac{\tan x+\tan h}{1-\tan x\tan h}\]. Substituting this formula, we get;
\[\begin{align}
  & h'\left( x \right)=\underset{h\to 0}{\mathop{\lim }}\,\left( \dfrac{\dfrac{\tan x+\tan h}{1-\tan x\tan h}-\tan x}{h} \right) \\
 & \Rightarrow h'\left( x \right)=\underset{h\to 0}{\mathop{\lim }}\,\left( \dfrac{\tan x+\tan h-\tan x\left( 1-\tan x\tan h \right)}{h\left( 1-\tan x\tan h \right)} \right) \\
 & \Rightarrow h'\left( x \right)=\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\tan x+\tan h-\tan x+{{\tan }^{2}}x\tan h}{h\left( 1-\tan x\tan h \right)} \\
 & \Rightarrow h'\left( x \right)=\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\tan h}{h}\dfrac{\left( 1+{{\tan }^{2}}x \right)}{\left( 1-\tan x\tan h \right)} \\
\end{align}\]
Since the limit is with respect to $h$, we can take $1+{{\tan }^{2}}x$ out of the individual limit in the above equation.
$\Rightarrow h'\left( x \right)=\left( 1+{{\tan }^{2}}x \right)\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\tan h}{h\left( 1-\tanh \tan x \right)}........\left( I \right)$
In $\left( I \right)$, $\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\tan h}{h\left( 1-\tanh \tan x \right)}=\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\tan h}{h}.............\left( II \right)$.
Also, we have a formula$\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\tan h}{h}=1.......\left( III \right)$.

Substituting these limits from $\left( II \right)$ and $\left( III \right)$ in equation $\left( I \right)$, we get;
$h'\left( x \right)=1+{{\tan }^{2}}x$
Also, from trigonometry, we have a formula; $1+{{\tan }^{2}}x={{\sec }^{2}}x$.
$\Rightarrow h'\left( x \right)={{\sec }^{2}}x........\left( IV \right)$
Substituting $x=a$ in the equation $\left( IV \right)$, we get;
$h'\left( a \right)={{\sec }^{2}}a$
 If we draw the graph of $\Rightarrow h'\left( x \right)={{\sec }^{2}}x$

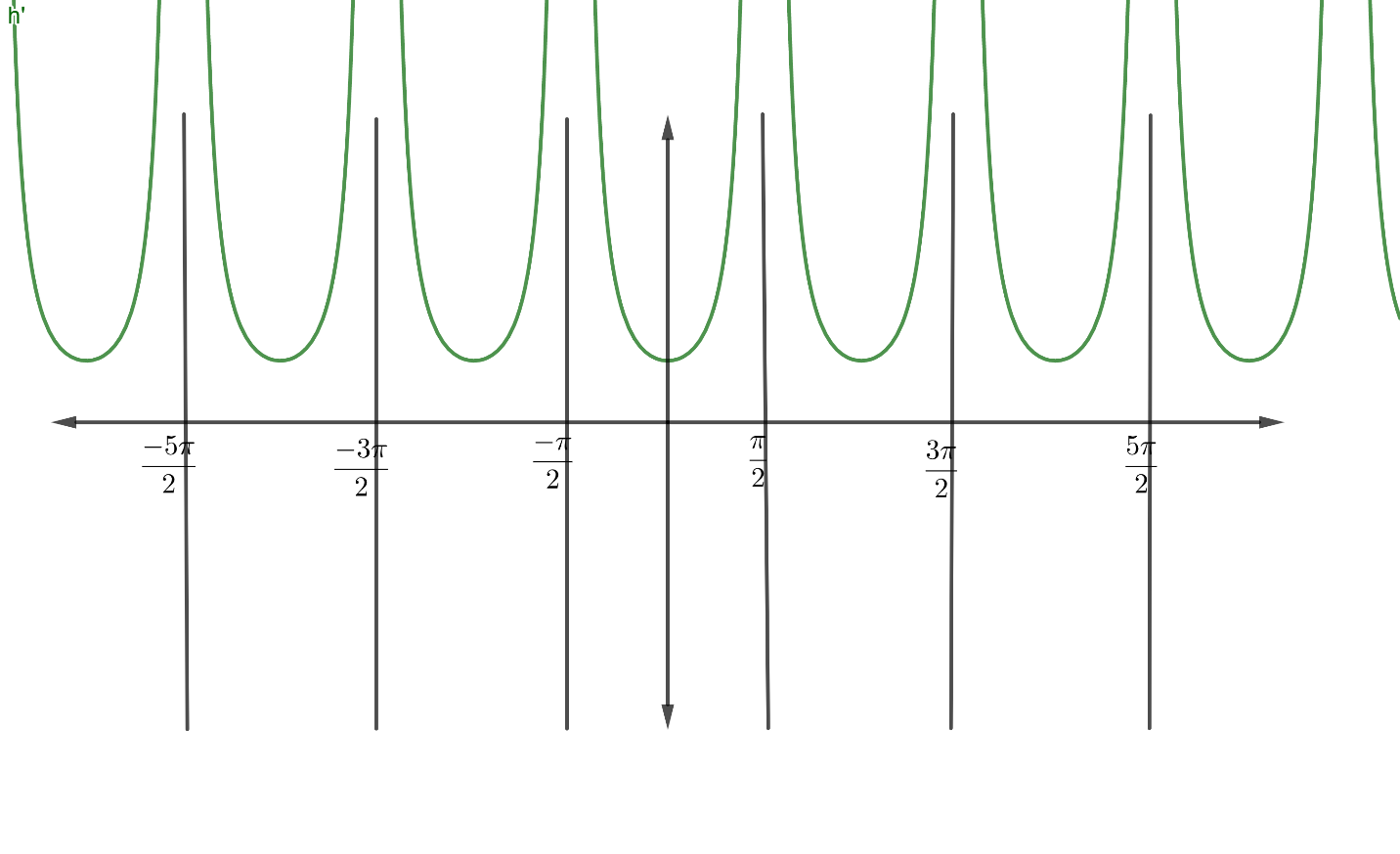
It can be observed that the graph of $h'\left( x \right)$ is discontinuous at $\left\{ ......\dfrac{-5\pi }{2},\dfrac{-3\pi }{2},\dfrac{-\pi }{2},0,\dfrac{\pi }{2},\dfrac{3\pi }{2},\dfrac{5\pi }{2},..... \right\}$
i.e., odd multiples of $\dfrac{\pi }{2}.$
This means that $h\left( x \right)$ is non-differentiable at odd multiples of $\dfrac{\pi }{2}.$
$\Rightarrow h\left( x \right)$ is differentiable for $x\in \mathbb{R}-\left\{ \text{odd multiple of }\dfrac{\pi }{2} \right\}$
Note: The question can be done directly if one knows the derivatives of $\tan x$ instead of finding the derivatives using the first principle of derivative.