Question

Show that the following points are collinear. $A(2, - 2),B( - 3,8)$ and $C( - 1,4)$.

Answer 1

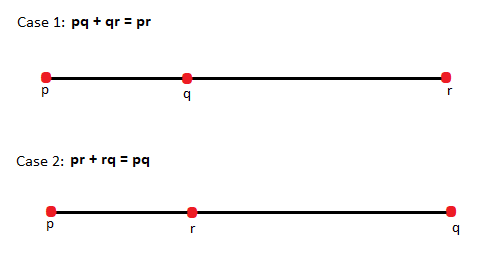
Hint: Collinear points are the points which lie on the same line. To check if the given points are collinear or not, here we will apply the distance formula to find the distance between the two points and check whether the sum of two measures is equal to the third measure. This can be understood by the following diagrams. Let p,q,r be any three collinear points, then

Complete step by step solution:
Here we will use the distance formula for the given points A and B, where
AB$ = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} $ then substitutes the value and simplify for the required resultant values.
For points $A(2, - 2),B( - 3,8),C( - 1,4)$will find measure between two points one by one
AB $ = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}} $
Place the values in the above expression –
AB$ = \sqrt {{{( - 3 - 2)}^2} + {{(8 - ( - 2))}^2}} $
Simplify the above expression –
AB $ = \sqrt {{{( - 5)}^2} + {{(10)}^2}} $
AB$ = \sqrt {25 + 100} $
AB$ = \sqrt {125} $
AB$ = 5\sqrt 5 $ ….. (A)
Similarly for the measures of other two points,
BC$ = \sqrt {{{( - 1 - ( - 3))}^2} + {{(4 - 8)}^2}} $
Simplify the above expression –
BC $ = \sqrt {{{( - 1 + 3)}^2} + {{( - 4)}^2}} $
BC$ = \sqrt {4 + 16} $
BC\[ = \sqrt {20} \]
BC$ = 2\sqrt 5 $ ….. (B)
Similarly,
CA\[ = \sqrt {{{(2 - ( - 1))}^2} + {{( - 2 - 4)}^2}} \]
Simplify the above expression –
CA $ = \sqrt {{{(2 + 1)}^2} + {{( - 6)}^2}} $
CA$ = \sqrt {9 + 36} $
CA$ = \sqrt {45} $
CA$ = 3\sqrt 5 $ ….. (C)
From equations, (A), (B) and (C)
We can write –
$
  AB = AC + BC \\
\Rightarrow 5\sqrt 5 = 3\sqrt 5 + 2\sqrt 5 \\
 $
Hence, we can say that all the given three points lie on the same line. So, they are collinear.

Note:
Be careful while simplifying and specially dealing with the two opposite signs that are positive and negative terms. Know the difference between the square and square-roots and apply them accordingly. Perfect square number is the square of an integer, just it is the product of the same integer with itself. For example - $25{\text{ = 5 }} \times {\text{ 5, 25 = }}{{\text{5}}^2}$, usually it is denoted by n to the power two i.e. ${n^2}$. Whereas square-root is well-defined as $\sqrt n $, for example \[25{\text{ = 5 }} \times {\text{ 5, }}\sqrt {{\text{25}}} {\text{ = }}\sqrt {{{\text{5}}^2}} = 5\].