Question

Show that $A\left( -1,0 \right),B\left( 3,1 \right),C\left( 2,2 \right)$ and $D\left( -2,1 \right)$ are the vertices of a parallelogram $ABCD$.

Answer 1

Hint: For solving this question first, with the help of the formula ${{m}_{AB}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ we will find the slope of the lines AB, BC, CD and DA. After that, we will use the concept that if two lines have equal value of the slope, then they will be parallel to each other for proving opposite sides of the quadrilateral ABCD are parallel and ultimately we will prove that ABCD will be a parallelogram.
Complete step by step answer:
Given:
We have to prove that points A (-1,0), B (3,1), C (2,2) and D (-2,1) are the vertices of a parallelogram ABCD.
Now, before we proceed we should know that in any quadrilateral if opposite sides are parallel then that particular quadrilateral will be a parallelogram, so we will use this property to prove that quadrilateral ABCD is a parallelogram.
Now, before we proceed we should know that slope of line AB through points $A\equiv \left( {{x}_{1}},{{y}_{1}} \right)$ and $B\equiv \left( {{x}_{2}},{{y}_{2}} \right)$ is ${{m}_{AB}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ and if two lines have equal value of the slope, then they will be parallel to each other.
Now, we come back to our problem in which we have points A (-1,0), B (3,1), C (2,2) and D (-2,1) so, with the help of the formula, ${{m}_{AB}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ we will find the slope of the lines AB, BC, CD and DA. Then,
$\begin{align}
  & {{m}_{AB}}=\dfrac{1-0}{3+1}=\dfrac{1}{4} \\
 & {{m}_{BC}}=\dfrac{2-1}{2-3}=-1 \\
 & {{m}_{CD}}=\dfrac{1-2}{-2-2}=\dfrac{-1}{-4}=\dfrac{1}{4} \\
 & {{m}_{DA}}=\dfrac{0-1}{-1+2}=-1 \\
\end{align}$
Now, from the above result, it is evident that the slope of the line AB and CD is equal, so they will be parallel lines. Moreover, the slope of the lines BC and DA is also equal, so they will be parallel lines also.
Now, we conclude that in quadrilateral ABCD opposite sides AB, CD are parallel and opposite sides BC, DA are also parallel. Then, we can say that quadrilateral ABCD will be a parallelogram. For more clarity look at the figure given below:

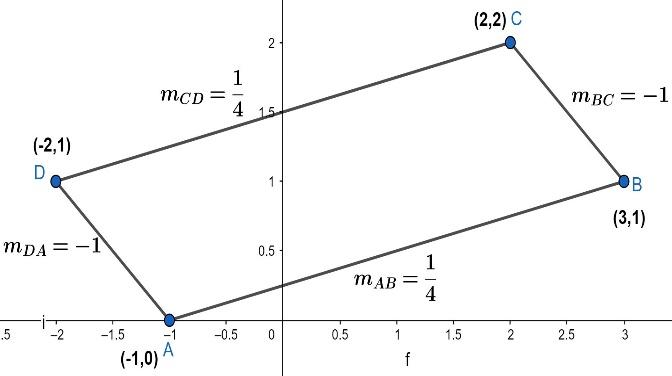
In the above figure parallelogram, ABCD is shown with the slopes of all the sides.
Hence, proved.

Note: Here, the student first understands what is asked in the question and then proceeds in the right direction to prove the desired result quickly. Moreover, though the question is very easy, we could have proved it using many other ways, but to minimise the calculation part we should use this method perfectly without any calculation mistakes. And in the end, we should plot the quadrilateral ABCD on the x-y plane for better understanding.