Question

Show in the figure are two point charges +Q and –Q are the inside the cavity of the spherical shell. The charges are kept near the surface of the cavity on opposite sides of the centre of the shell. If ${\sigma _1}$ is the surface charge on the inner surface and $Q_1$ net charge on it and ${\sigma _2}$ the surface and $Q_2$ net charge on them:
 

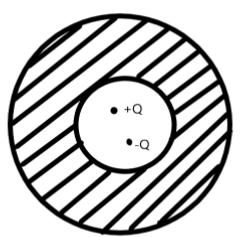
A. ${\sigma _1} \ne 0,{Q_1} = 0{\sigma _2} = 0,{Q_2} = 0$
B. ${\sigma _1} \ne 0,{Q_1} = 0{\sigma _2} \ne 0,{Q_2} = 0$
C. ${\sigma _1} \ne 0,{Q_1} \ne 0{\sigma _2} = 0,{Q_2} \ne 0$
D. ${\sigma _1} = 0,{Q_1} = 0{\sigma _2} = 0,{Q_2} = 0$

Answer 1

Hint: The zero field exists inside the cavity of a conductor. As the charge resides on the outer surface of a conductor, irrespective of any shape or size of the conductor, the field inside the cavity is always zero.

Complete answer:
Now from the question,
We are given charges ${Q_1}$ , ${Q_2}$ and surface charge density ${\sigma _1}$and ${\sigma _2}$ at the outer inner surface.
Now surface charge density $\sigma = \dfrac{q}{A}$ where q is the charge present on the surface and A is the area of the surface.
$\sigma = \dfrac{q}{{4\pi {r^2}}}$ where r is the radius of sphere
Since the net charge enclosed by a spherical shell is zero as all the charge is present on the surface
That is ${Q_1}$ , ${Q_2}$ =0
Therefore ${\sigma _1} = \dfrac{{{Q_1}}}{{4\pi {r^2}}}$=0
${Q_1} = 0and{\sigma _1} = 0$
And ${\sigma _2} = \dfrac{{{Q_2}}}{{4\pi {r^2}}}$=0
${Q_2} = 0,{\sigma _2} = 0$

Therefore the option (D) is the right answer.

Additional information:
Charge or we can say electric charge is a basic property of the electrons, the protons and the other subatomic particles. This binds electrons and protons together to form atoms. Important thing to remember is that the same charges push each other away. This is called the law of charges which is discovered by Charles-Augustin de coulomb.s discovered by Charles-Augustin de coulomb.

Note:
The charge is a scalar quantity as it has only magnitude and no direction. The charge is just as other fundamental properties of the system like mass. But the only difference between mass and the charge is that the charge has both positive as well as negative whereas in case of mass it has only positive.