Question

Show how \[\sqrt 5 \] can be represented on the number line.

Answer 1

Hint: We will first consider the given number which we have to represent on the number line. We will first draw the figure and draw the number line in it. We will mark two points 0 as O and 2 as A. After this draw a perpendicular at A and name the line as AX then mark a point at 1 unit on the perpendicular and mark it as the point B. Now, we will apply the Pythagoras theorem on the triangle OAB, and obtain the value of OB. Now, taking O as the center, we will cut the arc which will pass through the point B. The point on the right side of the point A that touches the number line will be the required point .

Complete step-by-step answer:
The objective is to represent \[\sqrt 5 \] on the number line.
We will first consider the number line which is made on the \[x\]-axis.
After this consider two points on the number line, zero is represented by O and 2 is represented as A. Now, draw a perpendicular on the point A and will name the line as AX.
Next, we will take 1 unit on the line AX and mark that point as B.
Now, we will apply the Pythagoras theorem on the triangle OAB and can find the value of line OB.
Thus, we have,
\[{\text{OA = 2}}\] and \[{\text{AB = 1}}\]
Hence,
\[
   \Rightarrow {\left( {{\text{OB}}} \right)^2} = {\left( {{\text{OA}}} \right)^2} + {\left( {{\text{AB}}} \right)^2} \\
   \Rightarrow {\left( {{\text{OB}}} \right)^2} = {\left( 2 \right)^2} + {1^2} \\
   \Rightarrow {\left( {{\text{OB}}} \right)^2} = 5 \\
   \Rightarrow {\text{OB}} = \sqrt 5 \\
 \]
Thus, we get the line OB as \[\sqrt 5 \] units.
Next, we will take O as the center and OB as \[\sqrt 5 \] units as radius draw an arc cut the point B and touch the point C on the right side of point A.
Thus, \[{\text{OC = OB = }}\sqrt 5 \].
Hence, the figure is shown as follows:

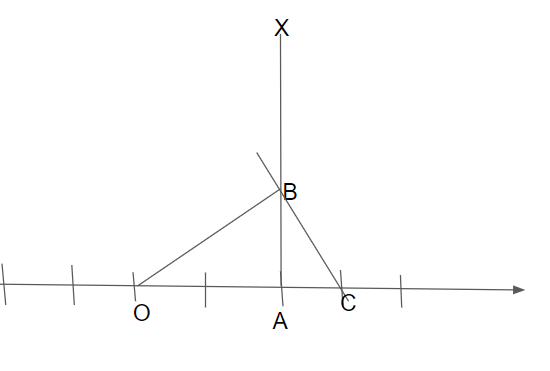
Thus, we can conclude that point C represents \[\sqrt 5 \] on the number line.

Note: Constructing a figure is important. The value of line OB can be evaluated using the Pythagoras theorem only as triangle OAB is a right-angled triangle. The arc cutting the point B will touch the point C on the number line.