Question

S and T are points on sides PR and QR of \[\Delta PQR\] such that ∠P=∠RTS. Show that \[\Delta RPQ\sim \]\[\Delta RTS\]

Answer 1

Hint: The AA similarity postulate is a shortcut for showing that two triangles are similar. If we know that two angles in one triangle are congruent to two angles in another, then we can say that the two triangles are similar. So in this problem we use AA similarity theorem to show that two triangles are similar.

Complete step-by-step answer:

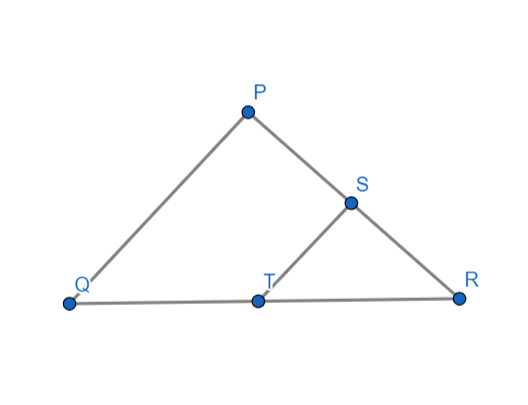
Given that the points S and T are on the sides of PR and QR such that ∠P=∠RTS
To prove that \[\Delta RPQ\sim \]\[\Delta RTS\]
Proof:
In \[\Delta RPQ\] and \[\Delta RTS\]
Given that ∠P=∠RTS. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (1)
And ∠PRQ=∠TRS= ∠R(common). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (2)
 From, equation (1) and equation (2) .So, by angle-angle or AA similarity
\[\Delta RPQ\sim \]\[\Delta RTS\]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ..(3)
Hence proved.

Note: There are so many theorems to show that two triangles are similar one among them is AA similarity and there is SSS theorem which states that two triangles are similar if the length of sides in one triangle are congruent to length of sides in another triangle and there is SAS theorem and SSA theorem and so on to prove that two triangles are similar