Question

Represent $ \sqrt {4.5} $ on the number line.

Answer 1

Hint: In this question, the first thing that you should do is to write down the definition of the number line, we read about in elementary mathematics. Fraction on the number line is important in order to understand how fraction represents part of a whole. We convert irrational no into rational no then represent on the number line.

Complete step-by-step answer:
In math, A number line can be defined as a straight line with numbers placed at equal intervals or segments along its length. A number line can be extended infinitely in any direction and is usually represented horizontally.
This is sample of number line

We find the rational no of $ \sqrt {4.5} $ is 2.12.
We break 2.12 step by step
First it lies on the number line in between 2 and 3. This is shown,

                                  

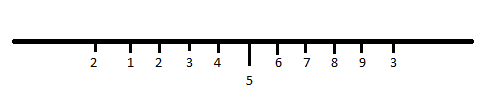
Then, 2.12 lies in 2 and 3 between 1 and 2 this is shown,
                                      

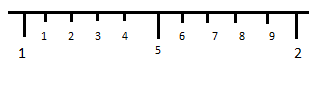
In between 1 and 2 nine line lies,
For showing 2.12 we use both number lines,

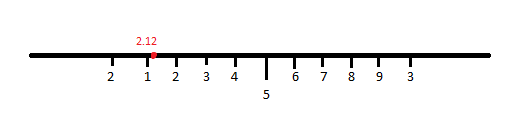
We represent 2.12 on number line like that,

Note – If a number is expressed in the form of p/q then it is a rational number; Here p and q are integers and q is not equal to zero some examples are 5,3,1/3 etc . Similarly if a number is not expressed in the form of p/q then it is a irrational number some examples are $ \sqrt 2 $ , $ \sqrt 5 $ , $ \sqrt {3.5} $ etc. zero is also a rational no because we express it in p/q form like that 0/1 =0.