
Represent \[ - \dfrac{7}{5}\] on the number line.
Answer
563.1k+ views
Hint:
The given rational number is an improper fraction. So, we will first convert it into a mixed fraction and check between which two integers it lies. Then we will divide the number line into the appropriate number of parts and mark the given rational number on the number line.
Complete Step by step Solution:
The given rational number is \[ - \dfrac{7}{5}\].
Since it is negative, it will lie on the left side of 0 on the number line.
Now, \[ - \dfrac{7}{5}\] is an improper fraction. So, to represent it on the number line, we will first convert it into a mixed fraction.
We see that \[ - \dfrac{7}{5} = - 1\dfrac{2}{5}\].
Here, \[ - 1\] is the whole part. So, \[ - \dfrac{7}{5}\] will lie between \[ - 1\] and the next integer which is \[ - 2\]. Thus, \[ - \dfrac{7}{5}\] lies between \[ - 1\] and \[ - 2\]. We will draw the number line as follows:

Since the denominator in \[ - \dfrac{7}{5}\] is 5, we will divide the space between \[ - 1\] and \[ - 2\] into 5 equal parts as follows:

Since \[ - \dfrac{7}{5} = - 1\dfrac{2}{5}\], we have to cross \[ - 1\] and mark \[\dfrac{2}{5}\] between \[ - 1\] and \[ - 2\]. Finally, we get:
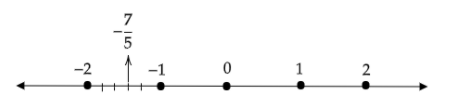
Note:
We can also represent \[ - \dfrac{7}{5}\] by converting it into a decimal value.
We observe that \[ - \dfrac{7}{5} = - 1.4\], which lies between \[ - 1\] and \[ - 2\].
We can also write \[1.4\] as
\[ - 1.4 = - 1 + 0.4 = - 1 + \dfrac{4}{{10}}\]
So, we can divide the space between \[ - 1\] and \[ - 2\] into 10 equal parts because the denominator in \[\dfrac{4}{{10}}\] is 10. The numerator is 4. Thus, we have to mark the 4th part in the 10 parts.
The given rational number is an improper fraction. So, we will first convert it into a mixed fraction and check between which two integers it lies. Then we will divide the number line into the appropriate number of parts and mark the given rational number on the number line.
Complete Step by step Solution:
The given rational number is \[ - \dfrac{7}{5}\].
Since it is negative, it will lie on the left side of 0 on the number line.
Now, \[ - \dfrac{7}{5}\] is an improper fraction. So, to represent it on the number line, we will first convert it into a mixed fraction.
We see that \[ - \dfrac{7}{5} = - 1\dfrac{2}{5}\].
Here, \[ - 1\] is the whole part. So, \[ - \dfrac{7}{5}\] will lie between \[ - 1\] and the next integer which is \[ - 2\]. Thus, \[ - \dfrac{7}{5}\] lies between \[ - 1\] and \[ - 2\]. We will draw the number line as follows:

Since the denominator in \[ - \dfrac{7}{5}\] is 5, we will divide the space between \[ - 1\] and \[ - 2\] into 5 equal parts as follows:

Since \[ - \dfrac{7}{5} = - 1\dfrac{2}{5}\], we have to cross \[ - 1\] and mark \[\dfrac{2}{5}\] between \[ - 1\] and \[ - 2\]. Finally, we get:

Note:
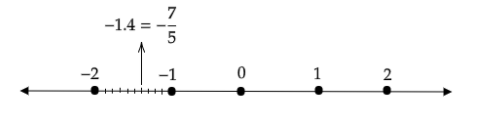
We can also represent \[ - \dfrac{7}{5}\] by converting it into a decimal value.
We observe that \[ - \dfrac{7}{5} = - 1.4\], which lies between \[ - 1\] and \[ - 2\].
We can also write \[1.4\] as
\[ - 1.4 = - 1 + 0.4 = - 1 + \dfrac{4}{{10}}\]
So, we can divide the space between \[ - 1\] and \[ - 2\] into 10 equal parts because the denominator in \[\dfrac{4}{{10}}\] is 10. The numerator is 4. Thus, we have to mark the 4th part in the 10 parts.

Recently Updated Pages
Master Class 6 Maths: Engaging Questions & Answers for Success

Master Class 6 English: Engaging Questions & Answers for Success

Master Class 6 Science: Engaging Questions & Answers for Success

Class 6 Question and Answer - Your Ultimate Solutions Guide

Master Class 6 Social Science: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples for herbs , shrubs , climbers , creepers

How many millions make a billion class 6 maths CBSE

What is the capital city of Australia? A) Sydney B) Melbourne C) Brisbane D) Canberra

What is the shape of Earth A Circle B Square C Sphere class 6 social science CBSE

The planet nearest to earth is A Mercury B Venus C class 6 social science CBSE

What are the main physical divisions of India class 6 social science CBSE





