Question

What is the relative velocity of car B with respect to car C?

Answer 1

Hint: We have been given the speed-time graph of three different cars in the problem. As we know, the slope of a speed-time graph gives us the speed. Thus, if we calculate the slope of all the expressions we can obtain the speed of the cars. Also, since the speed-time graph of all the cars is a straight line, it implies the speed is constant. So, we can use the formula of speed as distance by time also. We will be using a second method to solve our problem.

Complete answer:
Let us first assign some terms that we are going to use later in our equation.
Let the speed of car B be ${{v}_{B}}$. And,
Let the speed of car C be ${{v}_{C}}$.
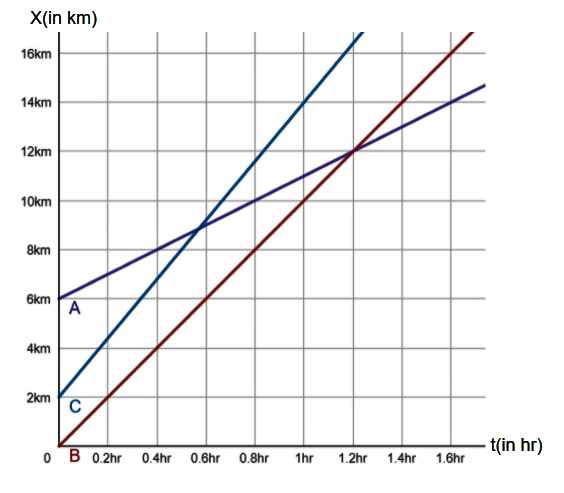
Then, from the speed-time graph, we can see that both the cars meet at a point $\left( 1.2hr,12km \right)$.
Let us use this point and the initial starting points of both the car B and C to calculate their respective velocities.
Now, for car B, we have:
$\begin{align}
  & \Rightarrow {{v}_{B}}=\dfrac{12-0}{1.2}kmh{{r}^{-1}} \\
 & \Rightarrow {{v}_{B}}=10kmh{{r}^{-1}} \\
\end{align}$
And, for car C, we have:
$\begin{align}
  & \Rightarrow {{v}_{C}}=\dfrac{12-6}{1.2}kmh{{r}^{-1}} \\
 & \Rightarrow {{v}_{C}}=5kmh{{r}^{-1}} \\
\end{align}$
Now, the relative velocity of the two cars can be calculated as follows:
$\begin{align}
  & \Rightarrow {{v}_{B}}-{{v}_{C}}=\left( 10-5 \right)kmh{{r}^{-1}} \\
 & \therefore {{v}_{B}}-{{v}_{C}}=5kmh{{r}^{-1}} \\
\end{align}$
Hence, the relative velocity of car B with respect to car C comes out to be $5kmh{{r}^{-1}}$.

Note:
We did not calculate the speed of car A as it was not a part of the problem and was just presented as extra information in the question. We should avoid such calculations to save our time. Also, one should practice enough to choose among different approaches to solve a problem, such that the chosen approach is the shortest and easiest.