Question

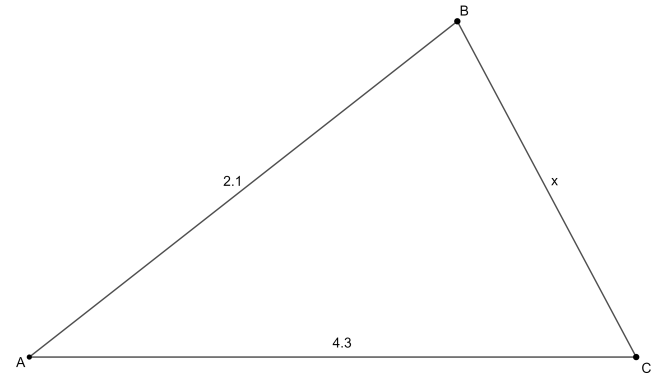
What is the range of possible sizes for side $x$?

(a) $1.2 < x < 6.4$
(b) $2.2 < x < 6.4$
(c) $-2.2 < x < 6.4$
(d) $2.1 < x < 6.4$

Answer 1

Hint: We will use the triangle inequality to find the range of possible sizes for side $x$. The triangle inequality says that the sum of any two sides of a triangle is greater than the third side. We will use this inequality two times to find the upper bound and lower bound of the possible size for side $x$.

Complete step-by-step answer:
The triangle inequality states that for any triangle, the sum of lengths of any two sides must be greater than the length of the remaining side.
In $\Delta ABC$, we will first look at the sum of side $AC$ and side $AB$. So, according to the triangle inequality we have $AC+AB>BC$. We know that $AC=4.3$, $AB=2.1$ and $BC=x$. Substituting these values in the inequality, we get
$\begin{align}
  & 4.3+2.1>x \\
 & \therefore x<6.4 \\
\end{align}$
So, we have found the upper bound for the size of $x$.
Now, we will look at the sum of side $AB$ and side $BC$. Using the triangle inequality, we have
$AB+BC>AC$.
Again, we will substitute the known values in the above inequality as follows,
$2.1+x>4.3$
Rearranging the above inequality, we get
$\begin{align}
  & x>4.3-2.1 \\
 & \therefore x>2.2 \\
\end{align}$
Therefore, we have found the lower bound for the size of $x$.
So, we have $2.2 < x < 6.4$. Hence, the correct option is (b).

So, the correct answer is “Option (b)”.

Note: It is essential that we know about the triangle inequality for solving this type of question. While rearranging the terms in the inequality, we should be careful about the signs of the term. We should write the inequalities explicitly to avoid any minor mistakes.