Question

Raghu walks around a park every day. How far does he walk in one round?
 

A. $198\text{ m}$
B. $\text{298 m}$
C. $228\text{ m}$
D. $\text{328 m}$

Answer 1

Hint: For finding out the distance walked around the park by Raghu , we will find out the perimeter of the park. We will do this by adding up all the sides given in the figure that is $P=AB+BC+CD+DA$. After adding the sides the resultant value will be our answer.

Complete step-by-step answer:
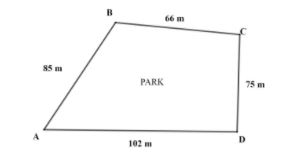
We are given a park where the sides of the park are as follows:
$\begin{align}
  & AB=85\text{ m} \\
 & BC=66\text{ m} \\
 & CD=75\text{ m} \\
 & DA=102\text{ m} \\
\end{align}$
We know that perimeter is defined as the length of the outline of a shape. If we want to find out the perimeter of a rectangle or square or any other quadrilateral shape (shapes with four sides and four vertices), all you have to do is add all the sides and get the perimeter of that shape.
Now to find out the total distance walked we will find out the perimeter of the park. Since we are given all the sides of the park the perimeter of the park will be as follows:
$P=AB+BC+CD+DA$ , where $P$ is the perimeter of the given park.
Now we will put the values of the sides in this equation, then we will get:
$\begin{align}
  & P=\left( 85+66+75+102 \right)\text{ m} \\
 & P=328\text{ m} \\
\end{align}$
Therefore, the total distance walked by Raghu around the park will be $328\text{ m}$ .

So, the correct answer is “Option D”.

Note: Any two dimensional figure will have its perimeter as sum of all its sides except the circle (the perimeter of a circle is called the circumference, it is equal to $2\pi r$, where $r$ is the radius of the circle.) If a given figure or polygon is regular means if its all sides are equal then the perimeter will be $n\times a$ , where n is the number of sides and a is the length of the side.