Question

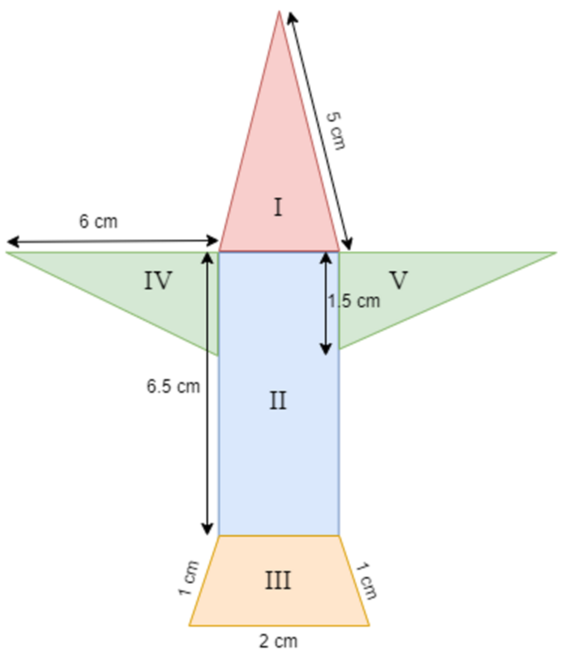
Radha made a picture of an airplane with colored paper as shown in Fig. Find the total area of the paper used.

Answer 1

Hint: The given figure is divided into five parts, part I is an isosceles triangle, part IV and part V are two right-angled triangles. Part II is a rectangle and part III is a trapezium.

Complete step-by-step solution
According to the question,
The given figure is divided into five different parts and in order to find the area of the figure we need to find the area of each part.
Area of first part = Area of isosceles triangle $ = \dfrac{b}{4}\sqrt {4{a^2} - {b^2}} $
Where b is the unequal side and a is the equal sides
Now substituting the value in the above equation, we get
Area of isosceles triangle $ = \dfrac{1}{4}\sqrt {4 \times {5^2} - 1} $
$ \Rightarrow $ Area of isosceles triangle $ = \dfrac{1}{4}\sqrt {100 - 1} = \dfrac{{\sqrt {99} }}{4} \approx 2.48$ …………… (i)
We know that Area of second part = Area of rectangle$ = l \times b$
Substituting the values, we get
Area of rectangle $ = 6.5cm \times 1cm = 6.5c{m^2}$ …………(ii)
Also, Area of third part = Area of trapezium
Since, Area of trapezium $ = \dfrac{1}{2}$ (sum of II sides) $ \times $ (distance between them)
Distance between II sides
$ = \sqrt {{1^2} - {{\left( {\dfrac{1}{2}} \right)}^2}} $
$ = \sqrt {1 - \dfrac{1}{4}} = \sqrt {\dfrac{3}{4}} = \dfrac{{\sqrt 3 }}{2}$
$ \Rightarrow $ Area of trapezium $ = \dfrac{1}{2}(2 + 1) \times \dfrac{{\sqrt 3 }}{2}c{m^2}$ $ = \dfrac{{3\sqrt 3 }}{4}c{m^2} = 1.3c{m^2}$ …………… (iii)
Area of fourth part $ = \dfrac{1}{2} \times base \times height$
Substituting the values, we get
Area of fourth part $ = \dfrac{1}{2} \times 1.5cm \times 6cm = 4.5c{m^2}$ …………… (iv)
Area of fifth part = Area of fourth part $ = 4.5c{m^2}$ ……………. (v)
Now, area of given figure = (i) + (ii) + (iii) + (iv) + (v) = (2.48 + 6.5 + 1.3 + 4.5 + 4.5)$c{m^2}$ $ = 19.28c{m^2}$
Therefore, the area of the given figure is $19.28c{m^2}$.

Note: To solve this type of question one must know the formulas of mensuration. For example, Area of isosceles triangle$ = \dfrac{b}{4}\sqrt {4{a^2} - {b^2}} $, where a is the equal sides and b is the base.
Area of trapezium $ = \dfrac{1}{2}$(sum of II sides) $ \times $ (distance between them).