Question

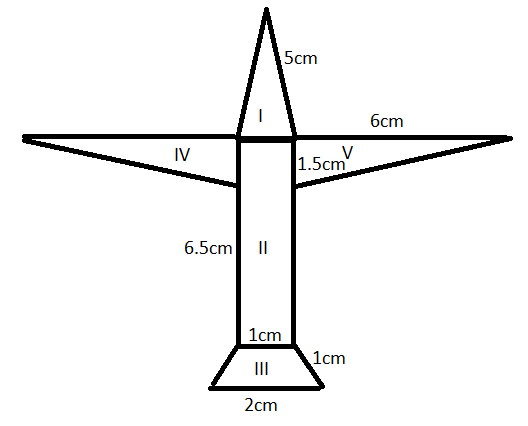
Radha made a picture of an aeroplane with coloured paper as shown. Find the total area of the paper used.

Answer 1

Hint:For solving this problem, we individually consider all the geometrical figures and find their respective areas. For obtaining the total area of paper used, we add all the areas obtained from geometrical figures.

Complete step-by-step answer:
Considering the figure given above, we divide the total area into 5 sub-parts.
Some of the useful formulas of area of geometrical figures can be stated as:
By using Heron's formula, area of triangle $=\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$
Area of rectangle $=l\times b$
Area of trapezium $=\dfrac{h}{2}\left( a+b \right)$
Now, considering the first figure which is a triangle having side length as 5 cm, 5 cm and 1 cm.

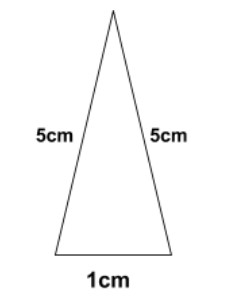
Use Heron’s formula to find area of figure,
The semi perimeter of a triangle is given as:
 $\begin{align}
  & s=\dfrac{5+5+1}{2} \\
 & s=\dfrac{11}{2} \\
 & s=5.5cm \\
\end{align}$
Now, applying the heron's formula, we get
$\begin{align}
  & =\sqrt{s(s-5)(s-5)(s-1)} \\
 & =\sqrt{5.5\times \left( 5.5-5 \right)\left( 5.5-5 \right)\left( 5.5-1 \right)} \\
 & =\sqrt{5.5\times 0.5\times 0.5\times 4.5} \\
 & =\sqrt{6.1875} \\
 & =2.487 \\
 & \approx 2.5c{{m}^{2}} \\
\end{align}$

Considering the figure 2 which is the rectangle having length 6.5 cm and breadth 1 cm.

 By using the above formula, the area of rectangle will be
$\begin{align}
  & =1\times 6.5 \\
 & =6.5c{{m}^{2}} \\
\end{align}$

Considering the figure 5 which is a triangle having side length as 6 and 1.5 cm. So, we first calculate the third side by using Pythagoras theorem $\left( {{a}^{2}}+{{b}^{2}}={{c}^{2}} \right)$.

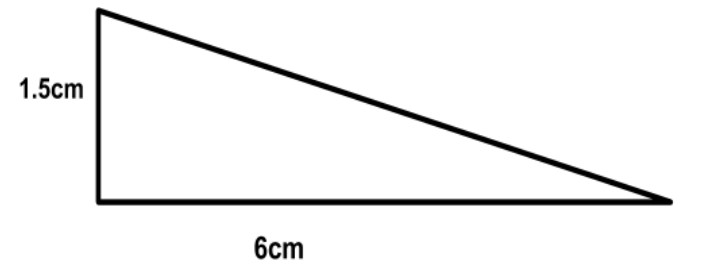
In the given triangle, a = 6 and b = 1.5, so for c:
$\begin{align}
  & {{c}^{2}}={{6}^{2}}+{{1.5}^{2}} \\
 & {{c}^{2}}=36+2.25 \\
 & {{c}^{2}}=38.25 \\
 & c=\sqrt{38.25}=6.184 \\
 & c\approx 6.2cm \\
\end{align}$
So, the length of the third side is 6.2 cm. Now, the semi perimeter of the triangle will be
$\begin{align}
  & s=\dfrac{6+1.5+6.2}{2} \\
 & s=\dfrac{13.7}{2} \\
 & s=6.85c{{m}^{2}} \\
\end{align}$
By applying the Heron's formula, we get
$\begin{align}
  & =\sqrt{s\left( s-6 \right)\left( s-1.5 \right)\left( s-6.2 \right)} \\
 & =\sqrt{6.85\left( 6.85-6 \right)\left( 6.85-1.5 \right)\left( 6.85-6.2 \right)} \\
 & =\sqrt{6.85\times 0.85\times 5.35\times 0.65} \\
 & =\sqrt{20.2445} \\
 & =4.499 \\
 & \approx 4.5c{{m}^{2}} \\
\end{align}$
 The area of the triangle obtained is 4.5 square cm.

Considering figure 4, it has the same area as that of figure 5. So, the area of figure 5 is 4.5 square cm.

Considering figure 3, the figure is trapezium whose parallel sides are 1cm and 2cm long. To
To calculate the height of the trapezium, we use Pythagoras theorem.

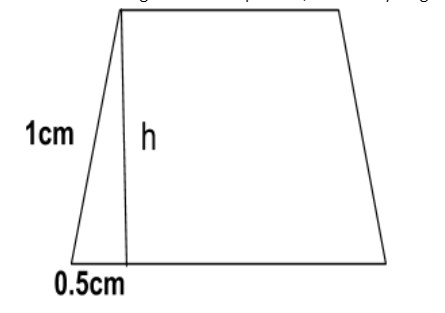
$\begin{align}
  & {{1}^{2}}={{h}^{2}}+{{0.5}^{2}} \\
 & {{h}^{2}}=1-0.25 \\
 & h=\sqrt{0.75} \\
 & h=0.8667 \\
 & h\approx 0.87cm \\
\end{align}$
The height of trapezium is 0.87 cm.
Therefore, by using the above stated formula the area of trapezium will be
$\begin{align}
  & =\dfrac{0.87}{2}\left( 1+2 \right) \\
 & =\dfrac{0.87}{2}\times 3 \\
 & =1.305c{{m}^{2}} \\
\end{align}$
So, the total area used for making the aeroplane = 2.5 + 6.5 + 4.5 + 4.5 + 1.305 = 19.305 square cm.

Note: Students must be careful while applying the various formulas. Approximation should be used in such a manner that it increases the value of area because paper could be larger than the actual area of aeroplane.