Question

Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its end by using the aluminium sheet. The diameter of the model is $3cm$ and its length is $12cm$ . if each cone has a height of $2cm$ , find the volume of air contained in the model that Rachel made.(Assume the outer and inner dimension of the model to be nearly the same).

Answer 1

Hint: The volume of the model can be determined by the addition of the respective volume of different shapes present in the model such as the model two shapes are present the first one is cylinder and the shape of cone but the cone in the model is two so the volume of cone will be doubled.

Complete step-by-step solution:
Let us consider the following shape to determine the result

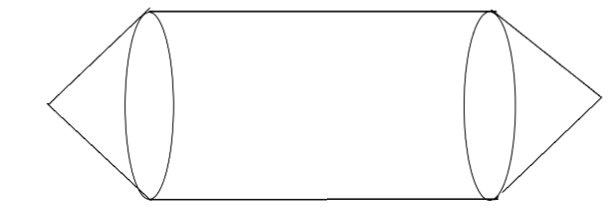
Hence, in the above figure we can see that the total height of the model is $12cm$ now we need to determine the height of the cylinder then in such case we will subtract the value of the length of the cone
Now, the height of one conical is $2cm$
 Similarly the height of the conical is also same
So, the total height of the conical is $4cm$
Since the diameter of the conical part is half of the diameter
Radius of the conical is $radius = \dfrac{{diameter}}{2}$
$radius = \dfrac{3}{2}cm$
Now, we need to determine the volume of the cone
$volume = \dfrac{2}{3}\left( {\pi {r^2}h} \right)$
We considered $\dfrac{2}{3}$ instead of $\dfrac{1}{3}$ because here we have to find the volume of 2 cones.
Now, substituting the required result, we get
$volume = \dfrac{2}{3}\left( {\pi {r^2}h} \right) = \dfrac{2}{3}\left( \pi \right){\left( {\dfrac{3}{2}} \right)^2}\left( 2 \right)$
Now, simplifying the above
$volume = \dfrac{2}{3}\left( {\pi {r^2}h} \right) = \dfrac{2}{3}\left( \pi \right){\left( {\dfrac{3}{2}} \right)^2}\left( 2 \right) = 3\pi $
Hence, the above is the required result for the volume of two cones
Now, we need to determine the volume of the cylinder
And to determine the volume of the cylinder we must have the information of the height of the cylinder and radius
Radius of the cylinder can be determined as follows
$radius = \dfrac{3}{2}cm$
Now, the height of the cylinder is the subtraction of the height of the cone from the total height to get the required result
$height = 12 - 2 - 2 = 8cm$
Hence, we get the required result to be equal to
The volume of the cylinder is
$volume = \pi {r^2}h$
Substituting the required value we get
$volume = \pi {r^2}h = \pi {\left( {\dfrac{3}{2}} \right)^2}8 = 18\pi $
The above represents the required volume of the model of cylinder
Now, we need to determine the total volume
${\text{total volume}} = 18\pi + 3\pi = 21\pi = 21\left( {\dfrac{{22}}{7}} \right) = 66c{m^2}$

The total volume of the given figure is $66c{m^2}$.

Note: Since we need to determine the whole volume of the model then in such case we need to determine the volume of cone and volume of cylinder and for the total volume we just add the two volumes together to get the required result.