
Put four different numbers in the circles so that when you add the numbers at the end of the line you always get a square.
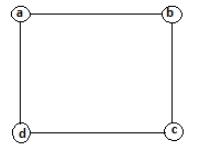

Answer
587.1k+ views
Hint: The values of the two circles, when added up, must give a number, which is square, whether horizontally or vertically. To solve the puzzle start substituting any number in the upper-left corner then put a number in the upper-right corner so that both numbers of the upper line of the square give a number, which is a square when added up.
Now put another number to the left bottom of the square so that the numbers of the left side vertically of the square give a square number.
Now also put a number to the bottom right corner of the square so that when the number is added with the number vertically or horizontally gives a square number.
Complete step by step answer:
Let a, b, c, and d be the numbers of corner elements.
Where \[a + b, b + c, c + d, d + a\] gives a square number
By hit and trial, method put the values of a, b, c, and d and check whether their sum gives a square number or not.
If we put
\[a = 1 \\
b = 3 \\
c = 46 \\
d = 35 \\\]
Then,
\[a + b = 1 + 3 = 4 = {2^2} \\
b + c = 3 + 46 = 49 = {7^2} \\
c + d = 46 + 35 = 81 = {9^2} \\
d + a = 35 + 1 = 36 = {6^2} \\\]
We get square numbers. Alternatively, if we put
\[a = 5 \\
b = 4 \\
c = 117 \\
d = 139 \\\]
Then,
\[a + b = 5 + 4 = 9 = {3^2} \\
b + c = 4 + 117 = 121 = {11^2} \\
c + d = 117 + 139 = 256 = {16^2} \\
d + a = 139 + 5 = 144 = {12^2} \\\]
Note: Students must note that when any two numbers are added, whether vertically or horizontally, in the square, the results should be a square number. In the question two geometrical shapes' names have been used i.e., circle and square, we need to put the numbers in the circle and keep the circle at the vertex of the square and the vice-versa does not hold true for this.
Now put another number to the left bottom of the square so that the numbers of the left side vertically of the square give a square number.
Now also put a number to the bottom right corner of the square so that when the number is added with the number vertically or horizontally gives a square number.
Complete step by step answer:

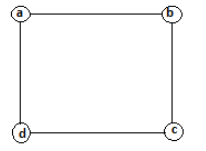
Let a, b, c, and d be the numbers of corner elements.
Where \[a + b, b + c, c + d, d + a\] gives a square number
By hit and trial, method put the values of a, b, c, and d and check whether their sum gives a square number or not.
If we put
\[a = 1 \\
b = 3 \\
c = 46 \\
d = 35 \\\]
Then,
\[a + b = 1 + 3 = 4 = {2^2} \\
b + c = 3 + 46 = 49 = {7^2} \\
c + d = 46 + 35 = 81 = {9^2} \\
d + a = 35 + 1 = 36 = {6^2} \\\]
We get square numbers. Alternatively, if we put
\[a = 5 \\
b = 4 \\
c = 117 \\
d = 139 \\\]
Then,
\[a + b = 5 + 4 = 9 = {3^2} \\
b + c = 4 + 117 = 121 = {11^2} \\
c + d = 117 + 139 = 256 = {16^2} \\
d + a = 139 + 5 = 144 = {12^2} \\\]
Note: Students must note that when any two numbers are added, whether vertically or horizontally, in the square, the results should be a square number. In the question two geometrical shapes' names have been used i.e., circle and square, we need to put the numbers in the circle and keep the circle at the vertex of the square and the vice-versa does not hold true for this.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Which Country is Called "The Land of Festivals"?

What is Contraception List its four different methods class 10 biology CBSE




