Question

Prove the relation \[a\cot A+b\cot B+c\cot C=2(R+r)\].

Answer 1

Hint: If we want to solve this question, then we must have knowledge of changing one trigonometric function into another trigonometric function, trigonometric rules, trigonometric identities. The question can be solved by taking the Left-Hand Side (L.H.S.) of the equation. First, we will convert cot function in terms of cos and sine functions. Then, we will use the sine rule. According to the Sine rule, \[\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R\]. After that, we will use the below trigonometric identities to simplify further and reach the answer,
\[\cos A+\cos B=2\cos \left( \dfrac{A+B}{2} \right)\cos \left( \dfrac{A-B}{2} \right)\]
\[\cos C=1-2{{\sin }^{2}}\dfrac{C}{2}\]
\[4\sin \dfrac{A}{2}\sin \dfrac{B}{2}\sin \dfrac{C}{2}=\dfrac{r}{R}\]

Complete step-by-step answer:
Now, we will solve the complete question.
Firstly, this equation needs to be proved. So for proving, we need to start from any one side of the equation and get the other side as a result of solving the first side.
So, for this question we will start the solution from the Left-hand Side (L.H.S.).
The L.H.S. of the equation is,
\[a\cot A+b\cot B+c\cot C\]
As we know, we can convert one trigonometric function to another trigonometric function, so here we will convert cot into sin and cos.
So, after converting, we will get,
\[a\dfrac{\cos A}{\sin A}+b\dfrac{\cos B}{\sin B}+c\dfrac{\cos C}{\sin C}\]

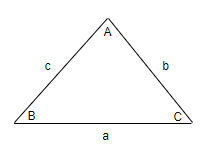
Now, if we apply Sine rule into this equation, we will get,
\[2R(\cos A+\cos B+\cos C)\]
Using the trigonometric identity of \[\cos A+\cos B=2\cos \left( \dfrac{A+B}{2} \right)\cos \left( \dfrac{A-B}{2} \right)\] and \[\cos C=1-2{{\sin }^{2}}\dfrac{C}{2}\], we will get,
\[\begin{align}
  & =2R\left[ 2\cos \left( \dfrac{A+B}{2} \right)\cos \left( \dfrac{A-B}{2} \right)+1-2{{\sin }^{2}}\dfrac{C}{2} \right] \\
 & =2R\left[ 1+2\cos \left( \dfrac{\pi }{2}-\dfrac{C}{2} \right)\cos \left( \dfrac{A-B}{2} \right)-2{{\sin }^{2}}\dfrac{C}{2} \right] \\
 & =2R\left[ 1+2\sin \left( \dfrac{C}{2} \right)\cos \left( \dfrac{A-B}{2} \right)-2{{\sin }^{2}}\dfrac{C}{2} \right] \\
 & =2R\left[ 1+2\sin \left( \dfrac{C}{2} \right)\left( \cos \left( \dfrac{A-B}{2} \right)-\sin \left( \dfrac{C}{2} \right) \right) \right] \\
 & =2R\left[ 1+2\sin \left( \dfrac{C}{2} \right)\left( \cos \left( \dfrac{A-B}{2} \right)-\sin \left( \dfrac{\pi }{2}-\dfrac{A+B}{2} \right) \right) \right] \\
 & =2R\left[ 1+2\sin \left( \dfrac{C}{2} \right)\left( \cos \left( \dfrac{A-B}{2} \right)-\cos \left( \dfrac{A+B}{2} \right) \right) \right] \\
\end{align}\]
Now, using the Transformation Angle formula, we get
\[\begin{align}
  & =2R\left[ 1+2\sin \left( \dfrac{C}{2} \right)2\sin \left( \dfrac{A}{2} \right)\sin \left( \dfrac{B}{2} \right) \right] \\
 & =2R\left[ 1+4\sin \left( \dfrac{A}{2} \right)\sin \left( \dfrac{B}{2} \right)\sin \left( \dfrac{C}{2} \right) \right] \\
 & =2R\left( 1+\dfrac{r}{R} \right) \\
 & =2(R+r) \\
\end{align}\]
The final answer which we got, matches the Right-Hand Side of the equation given in the question.
Hence, we proved the above equation.

Note: This question is full of theories which we have to keep in mind, if any student forgets any small thing in this question, then he or she may get many troubles while solving the question. This question can be done easily if we do and check every step after solving. Do not get confused in r and R, or interchange the places of r and R, as it may result in the wrong solution.