Question

Prove the following expression $\cos \left( 570{}^\circ \right)\sin \left( 510{}^\circ \right)+\sin \left( -330{}^\circ \right)\cos \left( -390{}^\circ \right)=0$.

Answer 1

Hint: We have to prove that the value of the given expression is 0. For that we can see that all the angles are not standard angles whose values are known to us. So, we have to first use formulas to convert them into standard forms. We can use the formulas, $\sin \left( -x \right)=-\sin x,\cos \left( -x \right)=-\cos x$ and also represent the angles such that they are in the form $\left( 360{}^\circ \pm \theta \right)$ to get the value of the angles.

Complete step-by-step answer:

It is given in the question that we have to prove the expression, $\cos \left( 570{}^\circ \right)\sin \left( 510{}^\circ \right)+\sin \left( -330{}^\circ \right)\cos \left( -390{}^\circ \right)=0$. To solve the question, we will first consider the left hand side or the LHS of the given expression. We know that $\sin \left( -x \right)=-\sin x$ and $\cos \left( -x \right)=\cos x$. So, we will substitute it in the given expression and get the LHS as,

$\cos \left( 570{}^\circ \right)\sin \left( 510{}^\circ \right)-\sin \left( 330{}^\circ \right)\cos \left( 390{}^\circ \right)$

Let us consider the quadrants first as below,

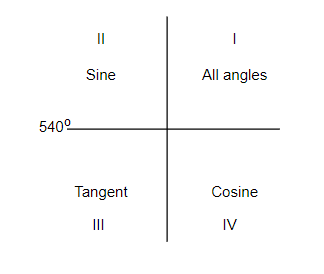
Now, we will solve each of the angles individually. So, we get,

$\begin{align}

  & \cos \left( 570{}^\circ \right)=\cos \left( 90{}^\circ \times 6+30{}^\circ \right) \\

 & =\cos \left( 540{}^\circ +30{}^\circ \right) \\

\end{align}$

We know that cos is positive in the first and the fourth quadrant. An angle $540{}^\circ
+\theta $ lies in the third quadrant. So, we get,

$=-\cos \left( 30{}^\circ \right)=-\dfrac{\sqrt{3}}{2}$

Similarly, we get,

$\begin{align}

  & \sin \left( 510{}^\circ \right)=\sin \left( 90{}^\circ \times 6-30{}^\circ \right) \\

 & =\sin \left( 540{}^\circ -30{}^\circ \right) \\

\end{align}$

We know that sin is positive in the first and the second quadrant. An angle $540{}^\circ
-\theta $ lies in the second quadrant. So, we get,

$=\sin \left( 30{}^\circ \right)=\dfrac{1}{2}$

Similarly, we get,

$\begin{align}

  & \sin \left( -330{}^\circ \right)=\sin \left( 90{}^\circ \times 4-30{}^\circ \right) \\

 & =\sin \left( 360{}^\circ -30{}^\circ \right) \\

\end{align}$

We know that, $\sin \left( 360-\theta \right)=-\sin \theta $, so applying that we get,

$=-\sin 30{}^\circ =-\dfrac{1}{2}$

Now, similarly, we get,

$\begin{align}

  & \cos \left( 390{}^\circ \right)=\cos \left( 90{}^\circ \times 4+30{}^\circ \right) \\

 & =\cos \left( 360{}^\circ +30{}^\circ \right) \\

\end{align}$

We know that, $\cos \left( 360-\theta \right)=\cos \theta $, so applying that we get,

$=\cos 30{}^\circ =-\dfrac{\sqrt{3}}{2}$

Now, putting all the values that we have obtained in the expression, we get,

$\begin{align}

  & =\left( -\dfrac{\sqrt{3}}{2} \right)\times \left( \dfrac{1}{2} \right)-\left( -\dfrac{1}{2} \right)\times \left( \dfrac{\sqrt{3}}{2} \right) \\

 & =-\dfrac{\sqrt{3}}{4}+\dfrac{\sqrt{3}}{4} \\

 & =0 \\

\end{align}$

Which is the same as the right hand side or the RHS of the given expression. Therefore LHS = RHS.

Hence, we have proved the given expression.


Note: The most common mistakes that the students make while solving this question is by putting the incorrect plus or minus signs of the value of the angles while doing the conversions. Therefore, it is advisable to go step by step while solving the question to reach the correct result and reduce the chances of error.