Question

Prove that two quadrilaterals are congruent to one another.

Answer 1

Hint: A quadrilateral is a polygon with four sides. Each quadrilateral has other properties that can be proved. Generally we have to put side’s interior angles of one quadrilateral in correspondence with sides and angles of another and to prove that all correspondence with sides and angles of another and to prove that all corresponding pairs of sides and angles are congruent.

Complete step by step solution:
Parallelogram theorem 1 states that each diagonal of a parallelogram divides the parallelogram into two congruent triangles.
Parallelogram theorem 2 states that the opposite sides of a parallelogram are congruent.
If we start drawing a generic parallelogram and assume the definition of parallelogram this means that all we know is that the shape is a quadrilateral with two pairs of parallel sides. The parallel lines give congruent angles which will prove that the triangles are congruent.
Since the opposite sides of the parallelogram are corresponding parts of the congruent triangles.

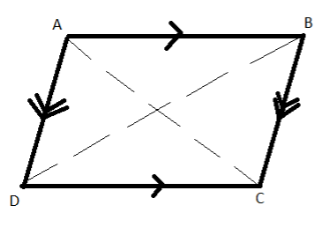
According to the definition of parallelogram,
\[\overline {AB} \left\| {\overline {DC} } \right.\] And\[\overline {AD} \left\| {\overline {BC} }
\right.\].
Since alternate interior angles are congruent if lines are parallel so we have reflexive property and hence AB is congruent to DC and AD is congruent to BC.
Both the theorems are proved now which states that quadrilaterals are congruent to one another.

Note: Each diagonal of a parallelogram divides the parallelogram into two congruent triangles and the opposite sides of a parallelogram are congruent. If a quadrilateral has opposite sides congruent then its diagonals divide the quadrilateral into congruent triangles. This proves that the quadrilateral is a parallelogram.