Question

Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.

Answer 1

Hint: Assume a circle with center O, radius R, and a tangent AB which touches at point P of the circle. Take any point Q, other than P, on the tangent AB. Join OQ. Suppose OQ meets the circle at point R. Now, we can write OQ as the summation of OR and RQ. We know that the OP and OR are the radius of the circle. So, OP = OR. We know the property that the shortest distance is the perpendicular distance. Using this property, conclude the answer.

Complete step-by-step answer:

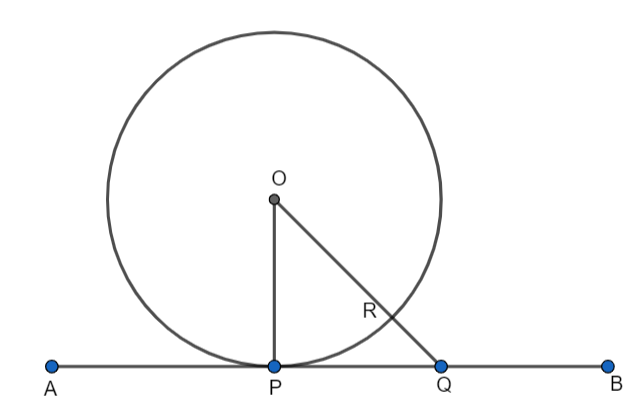
First of all, let us assume a circle with center O, R, and the line segment AB as the tangent to the circle at point P.
According to the question, we have to prove that the segment OP is perpendicular to the tangent AB.
Now, taking a point Q on the tangent AB, we have
OQ = OR + RQ ………………..(1)
We know that OP = OR because they are the radius of the same circle.
We can write equation (1) as,
OQ = OP + RQ
So, OQ>OP.
So, OP is possibly the shortest line segment than any other segment joining O to any point on AB.
We know that among all line segments joining the point O to a point on AB, the shortest one is perpendicular to AB.
Therefore, OP is perpendicular to AB.

Note: In this, question one can try to find \[\angle OPQ\] and make it equal to \[{{90}^{0}}\] . This approach is useless for this question because we don’t have sufficient data to find \[\angle OPQ\] . The only option that we have is to use the property that the shortest distance is the perpendicular distance.