Question

Prove that the sum of three altitudes of a triangle is less than the sum of three sides of the triangle.

Answer 1

- Hint: We will be using the concept of inequalities and Pythagoras theorem to solve the problem. We know that Pythagoras theorem states that in a right angle triangle.

Complete step-by-step solution -

Now, to prove the question given to us we will first draw a triangle ABC and its altitudes.

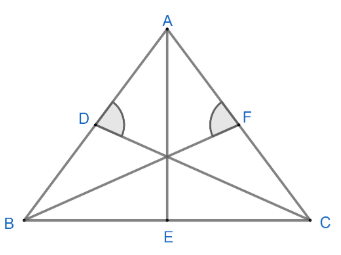
Now, In $\Delta AEC$ we will apply Pythagoras theorem.
So,
$\begin{align}
  & A{{C}^{2}}=A{{E}^{2}}+E{{C}^{2}} \\
 & A{{E}^{2}}=A{{C}^{2}}-E{{C}^{2}} \\
\end{align}$
Now, if we remove $-E{{C}^{2}}$ from right hand side then,
$A{{C}^{2}}$ will become greater than $A{{E}^{2}}$. Since, on subtracting $E{{C}^{2}}$ from $A{{C}^{2}}$ it was equal to $A{{E}^{2}}$. Therefore,
$\begin{align}
  & A{{E}^{2}} < A{{C}^{2}} \\
 & or\ AE < AC.........\left( 1 \right) \\
\end{align}$
Similarly, for $\Delta ABF$ by apply Pythagoras theorem we get,
$\begin{align}
  & A{{B}^{2}} = A{{F}^{2}}+B{{F}^{2}} \\
 & B{{F}^{2}} = A{{B}^{2}}-A{{F}^{2}} \\
 & B{{F}^{2}} < A{{B}^{2}} \\
 & BF < AB........\left( 2 \right) \\
\end{align}$
Now, applying Pythagoras theorem in $\Delta BDC$ we get,
$\begin{align}
  & B{{C}^{2}}=B{{D}^{2}}+D{{C}^{2}} \\
 & D{{C}^{2}}=B{{C}^{2}}-B{{D}^{2}} \\
 & D{{C}^{2}} < B{{C}^{2}} \\
 & DC < BC........\left( 3 \right) \\
\end{align}$
Now, we will add equation (1), (2) and (3),
$AE+BF+DC < AB+BC+CA$
Here, we know that AE, BF & DC are altitudes of triangle ABC.
Hence, prove that the sum of three altitudes of a triangle is less than the sum of three sides of a triangle.

Note: To solve these types of questions one must use inequalities of a triangle or make inequalities using Pythagoras theorem. Key words like less than requires attention to catch the question that is asking for an inequality.