Question

Prove that the sum of three altitude of a triangle is less than the sum of its sides

Answer 1

Hint: Altitudes are the perpendiculars from one side of a triangle to its opposite angle. There are three altitudes in a triangle. Perpendiculars are the lines that make the right angle $\left( {{{90}^ \circ }} \right)$ with the other line. Also, in a triangle if we compare any two angles and the sides opposite to these angles, the side opposite to the greater angle is greater than the other side.

Complete step by step solution:
Let us consider a triangle ABC. The altitude of this triangle is AD, BE, and CF and sides are AB, BC, and AC.

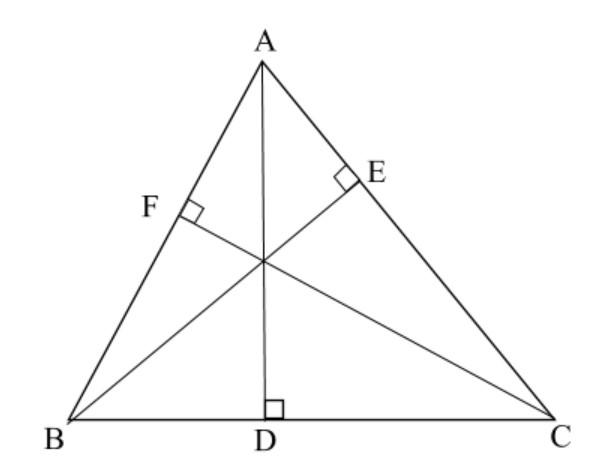
Now we consider the right $\vartriangle ABD$
$\angle ADB = 90^\circ $
and $\angle ABD$ is acute angle
$\therefore \angle ABD < 90^\circ $
Now side opposite to $\angle ADB$ is AB and side opposite to $\angle ABD$ is AD
Since side opposite to greater angle is greater
and $\angle ADB > \angle ABD$
$\therefore AB > AD\_\_\_\_\_\_\_\_\_\_\_\_\_\left( 1 \right)$
Now we consider right $\vartriangle BEC$
$\angle BEC = 90^\circ $
and $\angle BCE$ is acute angle
$\therefore \angle BCE < 90^\circ $
Now side opposite to $\angle BEC$ is BC and side opposite to $\angle BCE$ is BE
Since side opposite to greater angle is greater
and $\angle BEC > \angle BCE$
$\therefore BC > BE\_\_\_\_\_\_\_\_\_\_\_\_\_\left( 2 \right)$
Again we consider the right $\vartriangle AFC$
$\angle AFC = 90^\circ $
and $\angle FAC$ is acute angle
$\therefore \angle FAC < 90^\circ $
Now side opposite to $\angle AFC$ is AC and side opposite to $\angle FAC$ is CF
Since side opposite to greater angle is greater
and $\angle AFC > \angle FAC$
$\therefore AC > CF\_\_\_\_\_\_\_\_\_\_\_\_\_\left( 3 \right)$
Now we add three equations (1), (2) and (3) then we get
$ \Rightarrow \left( {AB + BC + AC} \right) > (AD + BE + CF)$
 $ \Rightarrow \left( {AD + BE + CF} \right) < (AB + BC + AC)$
$ \Rightarrow $sum of three altitudes < sum of three sides

Hence in any triangle the sum of three altitudes is less than the sum of its sides.

Note: Alternately,
We can also say that in any right-angled triangle, the hypotenuse is the biggest side. So, we can say
AB > AD (In triangle ADB) …………. (1)
BC > BE (In triangle BEC) …………… (2)
AC > CF (In triangle AFC) ……………. (3)
So, adding equation 1, 2 and 3, we get
AB + BC + AC > AD + BE + CF.