Question

Prove that the sum of the three angles in a triangle is equal to $180{}^\circ $.

Answer 1

Hint: We will first assume a triangle $ABC$. For this problem we will also construct a line which is parallel to the base and passing through the opposite vertex of the triangle. Now we will list out the alternative angles thus formed. Now we know that the angle on a horizontal line is $180{}^\circ $ so we will take an equation that is the sum of the angles on the horizontal line at the vertex and equate it to $180{}^\circ $. Now use the equations formed when we observed alternative angles and use then here to get the result.

Complete step by step answer:
Let $ABC$ is a triangle as shown in below figure.

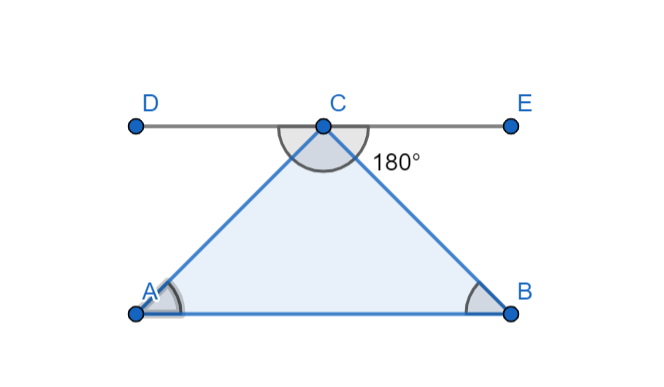
$DE$ is a line which is parallel to line $AB$ and passes through the vertex $C$ of the triangle $ABC$.
Now the alternative angles formed in the above diagram are
$\angle DCA=\angle CAB$
$\angle ECB=\angle CBA$
We know that the sum of the angle formed at a point on a horizontal line is equal to $180{}^\circ $.
$\therefore \angle DCA+\angle ACB+\angle ECB=180{}^\circ $
We have $\angle DCA=\angle CAB$ and $\angle ECB=\angle CBA$, substituting these values in the above equation then we will get
$\Rightarrow \angle CAB+\angle ACB+\angle CBA=180{}^\circ $
Now the sum of the three angles in the triangle $ABC$ is given by
$S=\angle CAB+\angle ACB+\angle CBA=180{}^\circ $
Hence Proved.

Note: We have the formula for the sum of the interior angles of the polygon with $n$ sides as $\left( 2n-4 \right)90{}^\circ $. From this formula we can calculate the sum of the interior angles of the triangle which is a polygon having $3$ sides, then we will get
$\begin{align}
  & S=\left( 2\times 3-4 \right)\times 90{}^\circ \\
 & \Rightarrow S=2\times 90{}^\circ \\
 & \Rightarrow S=180{}^\circ \\
\end{align}$
From both the methods we got the same result.