Question

Prove that the sum of the squares of the diagonals of a parallelogram is equal to the sum of squares of its sides.

Answer 1

- Hint:- Draw parallelogram ABCD, construct AX and BY perpendicular to base CD. Thus consider the triangle formed and by using Pythagoras theorem, find their relations to sides, such that \[B{{D}^{2}}+A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}+C{{D}^{2}}+D{{A}^{2}}\].

Complete step-by-step answer: -
Let us consider a parallelogram ABCD. We need to prove that the sum of squares of diagonals is equal to the sum of squares of its sides. Thus from the figure, we can say that we need to prove, \[B{{D}^{2}}+A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}+C{{D}^{2}}+D{{A}^{2}}\]
     

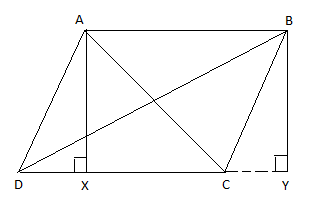
Now let us draw AX perpendicular to CD and BY perpendicular to CD extended to Y, i.e. draw \[AX\bot CD\] and \[BY\bot DC\].
Now let us consider \[\Delta AXC\].
\[A{{C}^{2}}=A{{X}^{2}}+C{{X}^{2}}........(1)\]
Consider the \[\Delta BYD\].
\[B{{D}^{2}}=B{{Y}^{2}}+D{{Y}^{2}}........(2)\]
Thus we got 2 equations,
\[A{{C}^{2}}=A{{X}^{2}}+C{{X}^{2}}\] and \[B{{D}^{2}}=B{{Y}^{2}}+D{{Y}^{2}}\].
From the figure, DY = CD + CY.
Thus in equation (2), \[B{{D}^{2}}=B{{Y}^{2}}+D{{Y}^{2}}=B{{Y}^{2}}+{{\left( CD+CY \right)}^{2}}\] \[\because {{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab\]
\[\therefore B{{D}^{2}}=\left( B{{Y}^{2}}+C{{Y}^{2}} \right)+C{{D}^{2}}+2CD.CY........(3)\]
Now from \[\Delta BYC\], if we take Pythagoras theorem, we get,
\[B{{C}^{2}}=B{{Y}^{2}}+C{{Y}^{2}}.......(4)\]
Thus substitute the value of equation (4) and (3).
\[\therefore B{{D}^{2}}=\left( B{{Y}^{2}}+C{{Y}^{2}} \right)+C{{D}^{2}}+2CD.CY......(5)\]
Now let us consider equation (1).
\[A{{C}^{2}}=A{{X}^{2}}+C{{X}^{2}}\]
From figure, we can say that,
CD = CX + XD
\[\therefore \]CX = CD – DX \[\because {{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab\]
\[\begin{align}
  & \therefore A{{C}^{2}}=A{{X}^{2}}+{{\left( CD-DX \right)}^{2}} \\
 & A{{C}^{2}}=A{{X}^{2}}+C{{D}^{2}}+D{{X}^{2}}-2CD.DX \\
 & A{{C}^{2}}=\left( A{{X}^{2}}+D{{X}^{2}} \right)+C{{D}^{2}}-2CD.DX......(6) \\
\end{align}\]
Now from \[\Delta AXD\], by Pythagoras theorem, we get,
\[A{{D}^{2}}=A{{X}^{2}}+D{{X}^{2}}.....(7)\]
Then substitute the value of equation (7) in (5).
\[\therefore A{{C}^{2}}=A{{D}^{2}}+C{{D}^{2}}-2CD.DX\]
In a parallelogram, the opposite sides of a parallelogram are equal. Thus in parallelogram ABCD, we can write that, AB = CD.
\[\therefore A{{C}^{2}}=A{{D}^{2}}+A{{B}^{2}}-2CD.DX......(8)\]
Now consider equation (5) and (8).
\[\begin{align}
  & B{{D}^{2}}=B{{C}^{2}}+C{{D}^{2}}+2CD.CY \\
 & A{{C}^{2}}=A{{D}^{2}}+A{{B}^{2}}-2CD.DX \\
\end{align}\]
Now let us add both equations (5) and (8). We get,
\[\begin{align}
  & B{{D}^{2}}+A{{C}^{2}}=B{{C}^{2}}+C{{D}^{2}}+A{{D}^{2}}+A{{B}^{2}}+2CD.CY-2CD.DX \\
 & \therefore B{{D}^{2}}+A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}+C{{D}^{2}}+A{{D}^{2}}+2CD\left( CY-DX \right).......(9) \\
\end{align}\]
We need to prove that, CY = DX.
From the figure, let us consider \[\Delta AXD\] and \[\Delta BYC\].
\[\angle AXD=\angle BYC\], they are both \[{{90}^{\circ }}\] by construction.
AX = BY, the perpendicular drawn between two parallel lines are equal.
AD = BC, opposite sides of a parallelogram are equal.
\[\therefore \Delta AXD\cong \Delta BYC\], by SAS congruency.
SAS congruency states that when 2 sides and one angle of a triangle are equal to 2 sides and one side of another triangle, then both triangles are equal.
Thus, both triangles are equal, we can say that CY = DX.
Now put CY = DX in equation (9).
\[\begin{align}
  & B{{D}^{2}}+A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}+C{{D}^{2}}+D{{A}^{2}}+2CD.\left( CY-CY \right) \\
 & B{{D}^{2}}+A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}+C{{D}^{2}}+D{{A}^{2}}+2CD\times 0 \\
 & \Rightarrow B{{D}^{2}}+A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}+C{{D}^{2}}+D{{A}^{2}} \\
\end{align}\]
Hence we proved that the sum of squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.

Note:-To prove this, it is important that you construct \[AX\bot CD\] and \[BY\bot CD\]. We can only prove if this construction takes place. Hence remember not to skip this important step. If you miss it then the entire calculation will be wrong.