Question

Prove that the opposite angles of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.

Answer 1

Hint: To solve the question, we have to apply the angle at the centre theorem by assuming the angles made at the centre by the major and minor arcs of the circle. The theorem connects the angles of quadrilateral and the angle at the centre which will lead to prove the given statement.

Complete step by step answer:
The quadrilateral is circumscribing a circle which implies that the given quadrilateral is cyclic quadrilateral by definition.
Let the given quadrilateral be ABCD and \[\alpha ,\beta \] be the angles subtended at the centre of the circle by minor and major arcs of circle respectively.
The angles of the quadrilateral ABCD are \[\angle A,\angle B,\angle C,\angle D\] where \[\angle A,\angle C\] and \[\angle B,\angle D\] are pairs of opposite angles of the given quadrilateral.

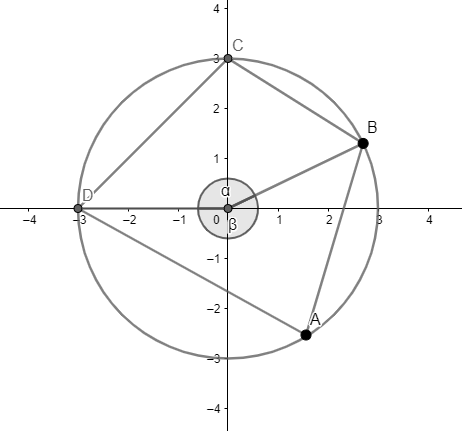
We know that the angle at the centre theorem which states that the angle subtended two chosen points on the centre of a circle is always twice the inscribed angle from those two points. Thus, by applying the theorem we get that,
The angle at centre by the major arc \[\beta \] is twice the angle \[\angle A\] .
The angle at centre by the minor arc \[\alpha \] is twice the angle \[\angle C\].
\[\Rightarrow \beta =2\angle A\] and \[\alpha =2\angle C\]
By adding the above two obtained equations we get
\[\beta +\alpha =2\angle A+2\angle C\]
We know that the angle of the circle is which implies \[\beta +\alpha ={{360}^{0}}\].
Thus, we get
\[2\angle A+2\angle C={{360}^{0}}\]
\[\angle A+\angle C=\dfrac{{{360}^{0}}}{2}={{180}^{0}}\] …….. (1)
We know that the sum of all the angles of the quadrilateral is equal to \[{{360}^{0}}\]
\[\Rightarrow \angle A+\angle B+\angle C+\angle D={{360}^{0}}\]
By applying the equation (1) to the above statement, we get
\[{{180}^{0}}+\angle B+\angle D={{360}^{0}}\]
\[\angle B+\angle D={{360}^{0}}-{{180}^{0}}\]
\[\Rightarrow \angle B+\angle D={{180}^{0}}\]
Thus, we get the sum of opposite angles of the given quadrilateral is equal to \[{{180}^{0}}\] which implies that these angles are supplementary.
Hence, proved.
Note: The possibility of mistake can be not using the angle at the centre theorem which is the most needed step to prove the given statement. and the Quadrilateral should be cyclic by definition.