Question

Prove that the line segment joining the midpoints of two sides of a triangle is parallel to the third side.

Answer 1

Hint: In this question, we use the properties of parallelogram. If one pair of opposite sides of a quadrilateral is equal and parallel then the quadrilateral is parallelogram.

Complete step-by-step answer:

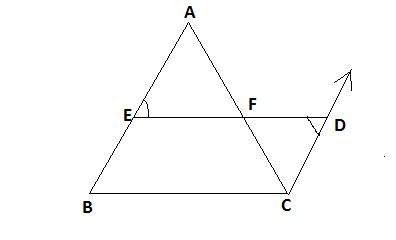
Given, ABC is a triangle where E and F are mid points of AB and AC respectively. So, AE=BE and AF=CF.
We have to prove: $EF\parallel BC$
Construction: Through C draw a line segment parallel to AB and extend EF to meet this line at D.
Now we know $AB\parallel CD$ , according to construction with transversal line ED.
$\angle AEF = \angle CDF$ (Alternate angle)
In $\vartriangle AEF{\text{ and }}\vartriangle CDF$
$
  \angle AEF = \angle CDF\left( {{\text{Alternate angle}}} \right) \\
  \angle AFE = \angle CFD\left( {{\text{vertically opposite angles}}} \right) \\
  AF = CF\left( {{\text{F is mid point of AC}}} \right) \\
  \vartriangle AEF \cong \vartriangle CDF\left( {AAS{\text{ rule}}} \right) \\
 $
So, EA=DC (CPCT)
As we know, EA=EB (E is midpoint)
Hence, EB=DC
Now, in quadrilateral BCDE
$EB\parallel CD{\text{ and }}EB = CD$
Thus, one pair of opposite sides is equal and parallel.
Hence, BCDE is a parallelogram.
Since opposite sides of parallelograms are parallel.
So, $ED\parallel BC$
We can write as, $EF\parallel BC$
So, it’s proved that the line segment joining the midpoints of two sides of a triangle is parallel to the third side.

Note-In such types of problems first we have to draw a figure and also construct a line parallel to one side of the triangle then prove construct quadrilateral is also a parallelogram and we know opposite sides of parallelogram are equal and parallel.