Question

Prove that the intercept of a tangent between two parallel tangents to a circle subtends a right angle at the center.

Answer 1

Hint: Line joining the parallel tangents will be straight line and will pass through the centre as well. Choose the triangles consisting of angles subtending at centre by the intercept of tangent and prove them congruent to each other. Draw a neat diagram to observe those triangles. Use the RHS property to prove the angles to be congruent. Angle by a straight line is \[{{180}^{\circ }}\].

Complete step-by-step solution -
Here, it is given that the tangents drawn are parallel and hence, we need to prove that the intercept of the tangent between two parallel tangents to a circle subtends at a right angle at centre.

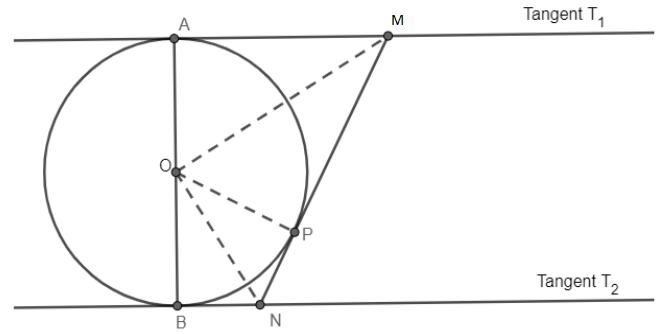
where OA, OB and OP are the radius of the circle and AM, BM, MN are parts of the tangents.

Now, it is given that the tangents ${{T}_{1}}$ and ${{T}_{2}}$ are parallel to each other.
It means line AB will be a straight line and angle AOB will be ${{180}^{\circ }}$ as per the property of parallel tangents in circle (proved in note part).
So, we get
$\angle AOB={{180}^{\circ }}..........(i)$
Now, we know the angle made at the touching point of the tangent to the circle, with the tangent and radius is ${{90}^{\circ }}$ , i.e. tangent and radius will be perpendicular to each other. So, we can write relations with tangents ${{T}_{1}},{{T}_{2}},$ MN and radius OA, OB and OP respectively as:
$\left. \begin{matrix}
   \angle OAM={{90}^{\circ }} \\
   \angle OBN={{90}^{\circ }} \\
   \angle OPN={{90}^{\circ }} \\
   \angle OPM={{90}^{\circ }} \\
\end{matrix} \right].........(iii)$
Now, in $\Delta AOM$ and $\Delta PON,$ we have
$\angle OAM=\angle OPM={{90}^{\circ }}$ [from equation (iii)]
OM=OM (common)
OA = OP = Radius (Radius of circle)
Hence, $\Delta AOM$ and $\Delta PON$ are congruent to each other by RHS property. Hence, we get
$\angle AOM=\angle MOP$ (By C.P.C.T)………(iv)
Similarly, we can prove angle NOP and angle BON as equal angles using the same approach.
As,
$\angle OBN=\angle OPN$ [from equation (iii)]
ON = ON (common)
OP=OB (radius)
Hence, $\Delta BON\cong \Delta PON$. So, we get
$\angle BON=\angle NOP$ (By C.P.C.T)…………..(v)
Now, we can observe the angle AOB which can be written as sum of angles $\angle AOM,\angle MOP,\angle NOP,\angle BON$ in following way:
$\angle AOB=\angle AOM+\angle MOP+\angle NOP+\angle BON$
Now, put $\angle AOB={{180}^{\circ }}$ from the equation (i) to the above expression. So we get
$\angle AOM+\angle MOP+\angle NOP+\angle BON={{180}^{\circ }}..........(vi)$
Now, we can replace $\angle MOP$ from equation (iv) and also can replace $\angle BON$ by $\angle NOP$ from equation (v). So, we get equation (vi) as
$\angle MOP+\angle MOP+\angle NOP+\angle NOP={{180}^{\circ }}$
$\Rightarrow 2\angle MOP+2\angle NOP={{180}^{\circ }}\,$
\[\Rightarrow 2\left( \angle MOP+\angle NOP \right)={{180}^{\circ }}\]
$\Rightarrow \angle MOP+\angle NOP=\dfrac{{{180}^{\circ }}}{2}={{90}^{\circ }}$
Now, we can replace $\angle MOP+\angle NOP$ by $\angle MON$ as both will be equal from the diagram. Hence, we get
$\angle MON={{90}^{\circ }}$
So, the angle subtended by the tangent MN is ${{90}^{\circ }}$.
Hence, the given statement is proved

Note: One may confuse with the statement that the line AOB will be straight and from angle as ${{180}^{\circ }}$

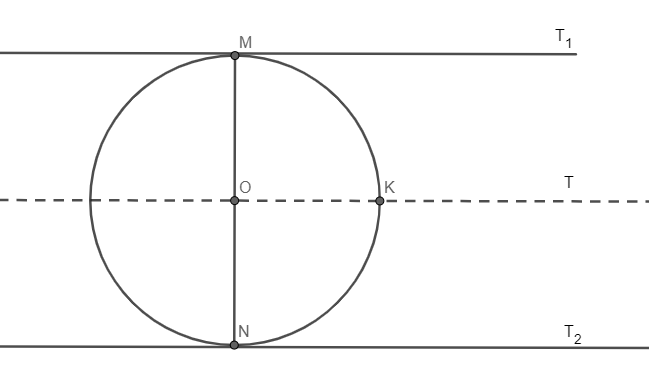
Proof:
Given: ${{T}_{1}}$ is parallel to ${{T}_{2}}$ and O is the centre of the circle
$\begin{align}
  & \angle OM{{T}_{1}}={{90}^{\circ }} \\
 & \angle ON{{T}_{2}}={{90}^{\circ }} \\
\end{align}$
Construction: Draw a line passing through centre O, and parallel to both the tangents ${{T}_{1}}$ and ${{T}_{2}}$
Proof:
As we know, angles made by transversal on the same side of two parallel lines has sum of ${{180}^{\circ }}$. So, OM is a transversal and tangent ${{T}_{!}}$ and line T are parallel to each other. So, we get
$\angle MOK+\angle OM{{T}_{1}}={{180}^{\circ }}$
$\begin{align}
  & \angle MOK+{{90}^{\circ }}={{180}^{\circ }} \\
 & \angle MOK={{90}^{\circ }} \\
\end{align}$
Similarly, $\angle NOK={{90}^{\circ }}$
So, $\angle MON=\angle MOK+\angle NOK={{90}^{\circ }}+{{90}^{\circ }}={{180}^{\circ }}$
RHS criteria means one angle of both the triangles should be ${{90}^{\circ }}$, the hypotenuse side of both should be equal and one another side also be equal. So, don’t confuse with criteria applied for proving two triangles as congruent triangles.