Question

Prove that the function defined by \[f(x) = \tan x\] is a continuous function.

Answer 1

Hint: We prove continuity of the function \[\tan x\] by writing in its simpler form of fraction whose continuity is known.
* A continuous function is a function that is continuous on every point of its domain. Also, we can always check continuity by drawing a graph, where the function is continuous means there is no breaking point in the curve.

Complete step-by-step answer:
We know, \[\tan x = \dfrac{{\sin x}}{{\cos x}}\]
We know graph of \[\sin x\] looks like

     

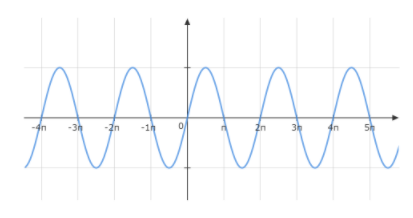
Since, there is no point where the curve breaks, so the function \[\sin x\] is continuous everywhere on R
Also, the graph of \[\cos x\] looks like.

     

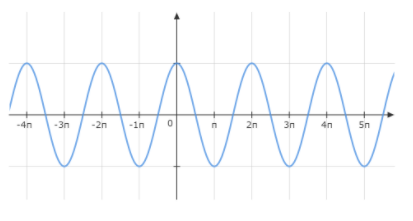
Since, there is no point where the curve breaks, so the function \[\cos x\] is continuous everywhere on R.
We know from the algebra of continuous functions that if both \[p(x)\] and \[q(x)\] are continuous functions then the function defined by their fraction \[f(x) = \dfrac{{p(x)}}{{q(x)}}\] is also continuous for all R such that \[q(x) \ne 0\]
Let us assume \[p(x) = \sin x\] and \[q(x) = \cos x\]
Then by Algebra of continuous functions \[f(x) = \dfrac{{\sin x}}{{\cos x}}\] is also continuous everywhere except at points where \[q(x) \ne 0\]
\[ \Rightarrow f(x) = \tan x\] is continuous everywhere except at points where \[q(x) \ne 0\]
Now we find points where \[ \Rightarrow f(x) = \tan x\] is not continuous.
We have \[q(x) \ne 0 \Rightarrow \cos (x) \ne 0\]
We will take all other values on R except where the values of \[\cos x\] become zero because if we make the denominator zero will make the fraction undefined.
\[
  \cos (x) \ne 0 \\
  \cos x \ne \cos (2n + 1)\dfrac{\pi }{2} \\
  x \ne (2n + 1)\dfrac{\pi }{2} \\
 \] {Since, all odd multiples of \[\dfrac{\pi }{2}\] will result in \[\cos x = 0\] }
So, \[ \Rightarrow f(x) = \tan x\] is continuous everywhere except at the points \[x = (2n + 1)\dfrac{\pi }{2}\], \[n = 0,1,2.....\]
Hence Proved
We can draw the graph of the function \[\tan x\]

     

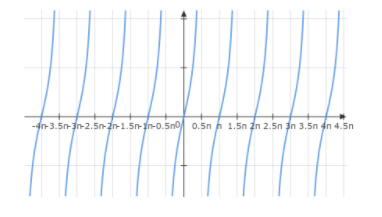
which is continuous everywhere except all the odd multiples of \[\dfrac{\pi }{2}\]

Note: Students many times get confused and write all multiples of \[\dfrac{\pi }{2}\] have function discontinuous ate them which is wrong, because when we take even multiples of \[\dfrac{\pi }{2}\], the angles becomes a multiple of \[\pi \] and which makes \[\cos \pi = - 1\] but we are finding values of x which make \[\cos x = 0\], so keep in mind we only take odd multiples of \[\dfrac{\pi }{2}\] only.