Question

Prove that the difference between the extreme tensions (or normal forces) depends only upon the weight of the objects.

Answer 1

Hint: We need to prove that difference between extreme tensions that is at opposite ends depends upon only the weight of the objects. In order to prove this, we have to assume a problem and then arrive at its solution. We consider a body tied to a string in a vertical circle.

Complete step by step answer:

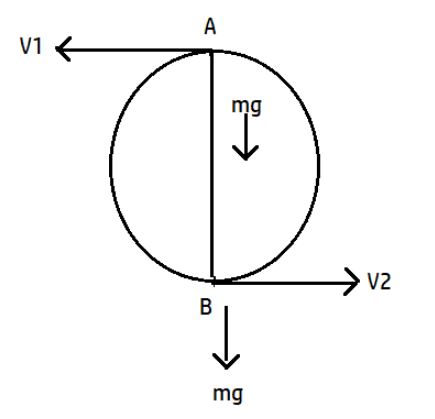
Assuming a mass m, tied to an inextensible string of length l, and it is being rotated in a vertical circle. During the circular motion one force acts towards the centre which is called centripetal force given by \[\dfrac{m{{v}^{2}}}{r}\], here v is the linear velocity of the body.
We take two diametrically opposite point at the circle say A and B. Let the two tensions in the string at point A and B be \[{{T}_{1}} \And {{T}_{2}}\] respectively.
Let \[{{v}_{1}}\] and \[{{v}_{2}}\] be the velocities at point A and B respectively.
At top most point A:
\[{{T}_{1}}+mg=\dfrac{mv_{1}^{2}}{r}\] ----------(1)
It has both kinetic and potential energy at A because I had taken the reference point as B, so, total energy at A is
\[\begin{align}
& {{E}_{1}}=mg(2r)+\dfrac{mv_{1}^{2}}{2} \\
&\Rightarrow {{E}_{1}}=2mgr+\dfrac{mv_{1}^{2}}{2} \\
\end{align}\]
At bottom most point B:
\[{{T}_{2}}-mg=\dfrac{mv_{2}^{2}}{r}\] --------(2)
It has only kinetic energy at B, \[{{E}_{2}}=\dfrac{mv_{2}^{2}}{2}\]
Assuming that the total energy of the body is conserved, the total energy at the bottom = total energy at the top
\[{{E}_{1}}={{E}_{2}}\]
\[\Rightarrow 2 mgr+\dfrac{mv_{1}^{2}}{2}=\dfrac{mv_{2}^{2}}{2}\]
\[\Rightarrow v_{2}^{2}-v_{1}^{2}=4gr\]----------(3)
Now subtracting (2) from (1) we get,
\[\begin{align}
&\Rightarrow \dfrac{mv_{2}^{2}}{r}-\dfrac{mv_{1}^{2}}{r}=-2mg+{{T}_{2}}-{{T}_{1}} \\
&\Rightarrow \dfrac{m}{r}(v_{2}^{2}-v_{1}^{2})=-2mg+{{T}_{2}}-{{T}_{1}} \\
& \\
\end{align}\]
Using value from eq (3)
\[\begin{align}
& \dfrac{m}{r}(4gr)=-2mg+{{T}_{2}}-{{T}_{1}} \\
&\Rightarrow 4mg+2mg={{T}_{2}}-{{T}_{1}} \\
&\therefore {{T}_{2}}-{{T}_{1}}=6mg \\
\end{align}\]

Therefore, the difference in the tensions in the string at the highest and the lowest points is 6 times the weight of the body.

Note:Here at the top most point centripetal force is equal to the sum of wight and tension and similar at the bottom most point centripetal force is equal to the sum of wight and tension. We have to be careful while looking at the directions otherwise our answer will not come correct.