Question

Prove that the diagonals of a parallelogram bisect each other.

Answer 1

Hint: Assume a parallelogram ABCD such that AC and BD are its diagonals intersecting at point O. We know the property that the opposite sides of a parallelogram are parallel and equal to each other. So, \[AD\parallel BC\] and \[AD=BC\] . We also know that the alternate interior angles of two parallel lines are equal to each other. So, \[\angle OAD=\angle OCB\] and \[\angle ODA=\angle OBC\] . Now, in \[\Delta OAD\] and \[\Delta OBC\] , we have \[AD=BC\] , \[\angle OAD=\angle OCB\] , and \[\angle ODA=\angle OBC\] . Check for the congruency. Then, solve it further and prove that, \[OD=OB\] and \[OA=OC\] .

Complete step-by-step answer:
First of all, let us assume that ABCD is a parallelogram, and AC and BD are its diagonals that are intersecting at point O.

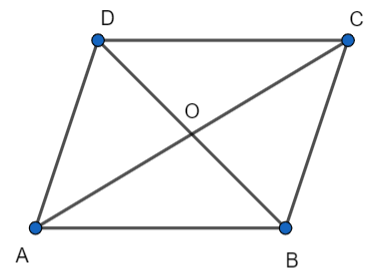
We know the property that the opposite sides of a parallelogram are parallel and equal to each other.
Using this property, we can say that the sides AD and BC of the parallelogram ABCD are parallel and equal to each other.
So, \[AD\parallel BC\] and \[AD=BC\] ………………………………………(1)
We know that the alternate interior angles of two parallel lines are equal to each other.
Since the sides AD and BC are parallel to each other,\[AD\parallel BC\] and the diagonal BD is the transversal so,
\[\angle OAD=\angle OCB\] (alternate interior angles) ……………………………………………(2)
Similarly, the sides AD and BC are parallel to each other,\[AD\parallel BC\] and the diagonal AC is the transversal so,
\[\angle ODA=\angle OBC\] (alternate interior angles) ……………………………………………(3)
Now, in \[\Delta OAD\] and \[\Delta OBC\] , we have
\[AD=BC\] (from equation (1))
\[\angle OAD=\angle OCB\] (from equation (2))
\[\angle ODA=\angle OBC\] (from equation (3))
So, \[\Delta OAD\cong \Delta OBC\] (Angle side angle criteria).
We know that the sides corresponding to the equal angles of the congruent triangles are also equal to each other (congruent part of congruent triangles).
Since \[\Delta OAD\] and \[\Delta OBC\] are congruent to each other so, \[OD=OB\] and \[OA=OC\] (congruent part of congruent triangles).
Thus, the diagonals AC and BD are bisecting each other at point O.
Hence, proved.

Note: In this question, one might make a silly mistake while taking the congruent part of the congruent triangles. Here, after proving \[\Delta OAD\cong \Delta OBC\] , one might take \[OD=OC\] and \[OA=OB\] as the congruent part of the congruent triangles. This is wrong because while taking the congruent part of the congruent triangles, we take those sides corresponding to equal angles as equal to each other. The angles corresponding to sides OD and OC are \[\angle OAD\] and \[\angle OBC\] . But these two angles are not equal so we cannot take the sides corresponding to these two angles as equal to each other. The sides corresponding to \[\angle OAD\] and \[\angle OBC\] are OD and OB. So, \[OD=OB\] (congruent part of congruent triangles).