Question

Prove that the area of trapezium is equal to half the product of sum of parallel sides and distance between the parallel sides.

Answer 1

Hint: The trapezium is a quadrilateral having two parallel sides known as bases and non-parallel sides of a trapezium are known as legs. We will divide the trapezium into three parts and we will find the area of different parts individually and add them to get the area of trapezium. Also, we will use the formula of area of a rectangle and area of a triangle which is as follows:
Area of triangle \[=\dfrac{1}{2}\times base\times height\]
Area of rectangle \[=length\times breadth\]

Complete step-by-step answer:
We have been asked to prove that the area of trapezium is equal to half of the product of the sum of the parallel sides and the distance between the parallel sides.
Let us suppose a trapezium ABCD having parallel sides equal to ‘a’ and ‘b’ and the height is equal to ‘h’.

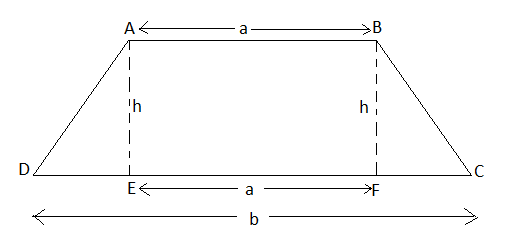
Now, area of trapezium ABCD = area of rectangle ABEF + area of triangle ADE + area of triangle BFC
We know that the area of a rectangle is equal to the product of its length and breadth.
\[\Rightarrow \]Area of rectangle ABEF \[=\left( a\times h \right)\] square units….(1)
Now in figure ABCD, let DE = x.
\[\begin{align}
  & \Rightarrow DE+EF+FC=b \\
 & \Rightarrow x+a+FC=b \\
 & \Rightarrow FC=b-(x+a) \\
\end{align}\]
Since we know the area of a triangle is equal to half of the product of base and height of a triangle
so area of triangle ADE,
\[\begin{align}
  & =\dfrac{1}{2}\times length\times breadth \\
 & =\dfrac{1}{2}\times DE\times AE \\
 & =\dfrac{1}{2}\times x\times h \\
\end{align}\]
\[\Rightarrow \]Area of \[\Delta ADE=\dfrac{xh}{2}\] square units…..(2)
Again, area of triangle BFC,
\[\begin{align}
  & =\dfrac{1}{2}\times length\times breadth \\
 & =\dfrac{1}{2}\times FC\times BF \\
\end{align}\]
\[\Rightarrow \]Area of \[\Delta BFC=\dfrac{1}{2}\times \left( b-(x+a) \right)\times h\]…..(3)
So by using equation (1), (2) and (3), we get as follows:
Area of trapezium ABCD,
\[\begin{align}
  & =\left( a\times h \right)+\dfrac{xh}{2}+\dfrac{1}{2}\left( b-(a+x) \right)\times h \\
 & =ah+\dfrac{xh}{2}+\dfrac{bh}{2}-\dfrac{ah}{2}-\dfrac{xh}{2} \\
 & =ah-\dfrac{ah}{2}+\dfrac{bh}{2} \\
\end{align}\]
Taking LCM of the terms, we get as follows:
\[=\dfrac{2ah-ah+bh}{2}=\dfrac{ah+bh}{2}=\dfrac{1}{2}(a+b)\times h\]
Hence it is proved that the area of a trapezium is equal to half the product of the sum of the parallel sides and the distance between the parallel sides.

Note: Be careful while finding the area of rectangle and triangle and also take care of the sign while doing the calculation. Also remember that it is not necessary that the non-parallel sides of trapezium are equal in length; it may be of different length. So, we have taken DE as x and FC as b - (x+a). If we consider the area of both the triangles as the same, it will not be correct.