Question

Prove that the area of a circular path of uniform width h surrounding a circular region of r is $\pi h\left( 2r+h \right)$.

Answer 1

Hint: Find the radius of the outer boundary of the path i.e. outer semi-circle by adding radius of inner semi-circle and width of the path. Area of a circle is given as $\pi {{r}^{2}}$ , where the value of $\pi $ is $\dfrac{22}{7}$ and r is the radius of the circle. Use ${{\left( a+b \right)}^{2}}={{\left( a \right)}^{2}}+\ {{\left( b \right)}^{2}}+\ 2ab$ wherever required. Area of the path is the difference of the area of outer and inner semi-circle.

Complete step-by-step answer:
Here, we have a circular region of radius ‘r’ and a circular path around it of width ‘h’.
So, we can draw a diagram with given information as

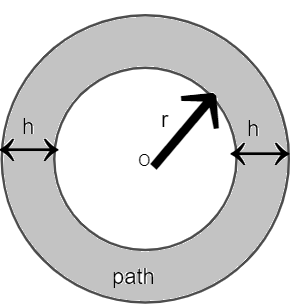
Now, we can observe that area of the path can be calculated by taking the difference of the area of the outer and inner circle, So, we get
Area of path = Area of outer circle - Area of inner circle ………………………………………..(i)
Now, we know that radius of any circle with radius ‘r’ can be given by relation $\pi {{r}^{2}}$, where value of $\pi $ is
$\dfrac{22}{7}$ and r is the radius of the circle.
As we observe that radius of the outer circle can be calculated by adding the radius ‘r’ of inner circle and width h of the path, so, radius of the outer circle is $\left( r+h \right)$. So, areas of outer and inner circle can be given as $\pi {{\left( r+h \right)}^{2}}$ and $\pi {{r}^{2}}$. Now, put the areas of outer and inner circle in equation (i). So, we get
Area of the path $=\ \pi {{\left( r+h \right)}^{2}}-\pi {{r}^{2}}$
Area of path $=\ \pi \left[ {{\left( r+h \right)}^{2}}-{{r}^{2}} \right]$ …………………………………………………………………………………………(ii)
Now, expand ${{\left( r+h \right)}^{2}}$ using the algebraic identity of ${{\left( a+b \right)}^{2}}$, which can be given as
${{\left( a+b \right)}^{2}}=\ {{a}^{2}}+{{b}^{2}}+2ab$…………………………………………………………………………(iii)
Hence, equation (iii) can be simplified further with the help of equation (iii) as
Area of path $=\ \pi \left[ {{r}^{2}}+{{h}^{2}}+2rh-{{r}^{2}} \right]$
$=\ \pi \left[ {{h}^{2}}+2rh \right]$
Now take ‘h’ as common from the expression. Hence, we get
Area of path $=\ \pi h\left[ h+2r \right]$ $\Rightarrow \pi h\left[ 2r+h \right]$
Hence, it is proved that the area of a circular path of uniform width ‘h’ surrounding a circular region ‘r’ is $\pi h\left[ 2r+h \right]$.

Note: Calculating radius of outer circle and hence, the area of path by taking the difference of the area of outer circle and inner circle are the key points of the question.
Don’t confuse the formula of area of circle and circumference of circle. One may use the formula of circumference in place of area by mistake. So, don’t confuse with them both are given as
Area of circle $=\ \pi {{r}^{2}}$
Circumference of circle $=\ 2\pi r$