Question

Prove that the adjacent angles of the parallelogram are supplementary.

Answer 1

Hint: Let us use the property of parallelogram that opposite sides of a parallelogram are parallel to each other.

Complete step-by-step answer:

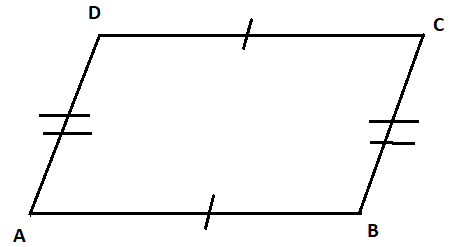
Let the above figure drawn ABCD be a parallelogram.

So, according to the properties of parallelogram.

Opposite sides of a parallelogram are parallel to each other and also equal to each other in length.

So, AB will be parallel to DC (i.e. AB || DC

And, AD will be parallel to BC (i.e. AD || DC).

As we know that if two lines are parallel and there is also a transversal to both lines then the sum of interior angles of the same side of the transversal will be equal to \[{180^0}\].

Now we can see that AD is the transversal to AB and DC. So, \[\angle {\text{A }} + {\text{ }}\angle {\text{D }} = {\text{ }}{180^0}\].

DC is the transversal to AD and BC. So, \[\angle {\text{D }} + {\text{ }}\angle {\text{C }} = {\text{ }}{180^0}\].

CB is the transversal to DC and AB. So, \[\angle {\text{C }} + {\text{ }}\angle {\text{B }} = {\text{ }}{180^0}\].

And, AB is the transversal to DA and CB. So, \[\angle {\text{A }} + {\text{ }}\angle {\text{B }} = {\text{ }}{180^0}\].

And we know that the sum of two angles is equal to \[{180^0}\]. Then those angles are supplementary to each other.

Hence, adjacent angles of parallelogram are supplementary.

Note: Whenever we come up with this type of problem then an efficient way to prove the result is by using the properties of parallelogram. And remember that if two lines are parallel then the sum of angles on the same side of the transversal of both lines is equal to \[{180^0}\].