Question

How do you prove that tangent is an odd function?

Answer 1

Hint: We first draw the graph of $\tan x$ . After that we take two lines $x={{60}^{\circ }}$ and $x=-{{60}^{\circ }}$ . We note the ordinates of the two points of intersection which are negative. So, $\tan x$ is an odd function.

Complete step-by-step answer:
Functions can be odd or even functions. According to definition, a function is said to be even if $f\left( -x \right)=f\left( x \right)$ , which means that irrespective of the sign (positive or negative) of the independent variable $x$ , the value of the function does not change. On the other hand, if $f\left( -x \right)=-f\left( x \right)$ , then the function is said to be an odd function, which means that as the sign of the independent variable $x$ changes, the sign of the function changes too.
In this given problem, we need to prove that tangent is an odd function. By tangent, we mean $\tan x$ . We can prove this statement graphically. We first draw the graph of $\tan x$ .

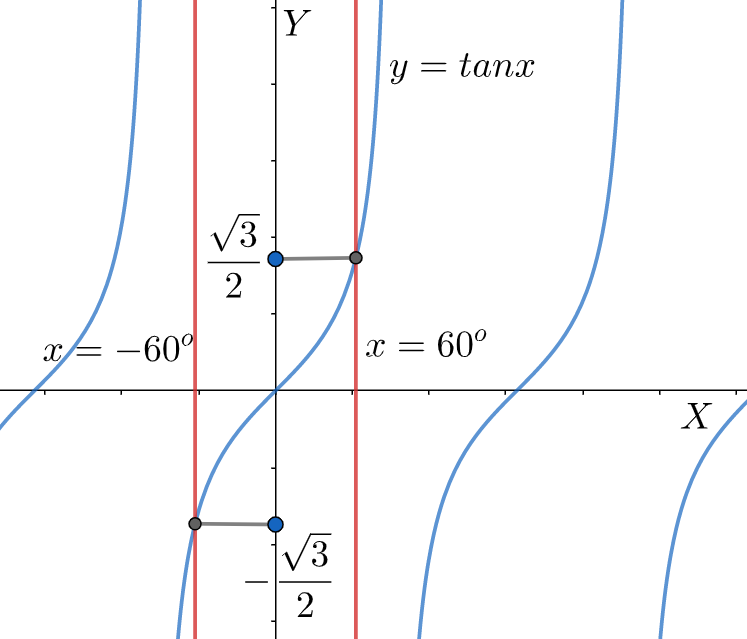
Let us first investigate the nature of the function at some $x>0$ , say ${{60}^{\circ }}$ . So, we need to take $x={{60}^{\circ }}$ line. The point where this $x={{60}^{\circ }}$ line cuts the $\tan x$ graph is $\left( {{60}^{\circ }},\dfrac{\sqrt{3}}{2} \right)$ , which means that the value of $\tan x$ is positive at $x={{60}^{\circ }}$ .
We see that the value of $\tan x$ at ${{60}^{\circ }}$ is positive. Now, we need to take another $x<0$ whose magnitude is equal to the previous positive $x$ taken. So, we need to take the $x=-{{60}^{\circ }}$ line. The point where this $x=-{{60}^{\circ }}$ line cuts the $\tan x$ graph is $\left( -{{60}^{\circ }},-\dfrac{\sqrt{3}}{2} \right)$ . This means that the value of $\tan x$ is negative at $x=-{{60}^{\circ }}$ .
Therefore, we can prove that tangent is an odd function as the two values of $\tan x$ at two values of $x$ , one being positive and the other being negative, are of opposite signs.

Note: The graph of $\tan x$ should be drawn correctly. We should remember to take only two such values of $x$ which have equal magnitude but opposite signs. We can also have the traditional method of proving it odd by showing that $\tan x$ is negative in the fourth quadrant, thus it is an odd function.