Question

Prove that $\sin \left( 90+\theta \right)=\cos \theta $ ?

Answer 1

Hint: We start off with the trigonometric formula $\sin \left( A+B \right)=\sin A\cos B+\cos A\sin B$ . In this formula, we put the value of A as ${{90}^{\circ }}$ and that of B as $\theta $ . The equation becomes $\Rightarrow \sin \left( {{90}^{\circ }}+\theta \right)=\sin {{90}^{\circ }}\cos \theta +\cos {{90}^{\circ }}\sin \theta $ . Putting the values of $\sin {{90}^{\circ }}$ and $\cos {{90}^{\circ }}$ as $1$ and $0$ respectively, we get the required identity.

Complete step by step answer:
Trigonometry is a branch of mathematics that studies relationships between side lengths and angles of triangles. Trigonometry is known for its many identities. These trigonometric identities are commonly used for rewriting trigonometric expressions with the aim to simplify an expression, to find a more useful form of n expression, or to solve an equation.
 In this problem, we need to prove a trigonometric identity. The identity is $\sin \left( 90+\theta \right)=\cos \theta $ . In order to prove this, we need the help of some other trigonometric formula. The formula is as follows,
$\sin \left( A+B \right)=\sin A\cos B+\cos A\sin B$
In our problem, the value of A is ${{90}^{\circ }}$ and that of B is $\theta $ . So, replacing A with ${{90}^{\circ }}$ and B with $\theta $ in the above formula, we get,
$\Rightarrow \sin \left( {{90}^{\circ }}+\theta \right)=\sin {{90}^{\circ }}\cos \theta +\cos {{90}^{\circ }}\sin \theta $
Now, we know the value of $\sin {{90}^{\circ }}$ and $\cos {{90}^{\circ }}$ . The values are $1$ and $0$ respectively. So, putting these values in the above equation, we get,
$\Rightarrow \sin \left( {{90}^{\circ }}+\theta \right)=1\left( \cos \theta \right)+0\left( \sin \theta \right)$
Simplifying the above equation, we get,
$\Rightarrow \sin \left( {{90}^{\circ }}+\theta \right)=\cos \theta +0$
The above equation is nothing but,
$\Rightarrow \sin \left( {{90}^{\circ }}+\theta \right)=\cos \theta $
Thus, we can conclude that the trigonometric identity of the given problem has been proved.

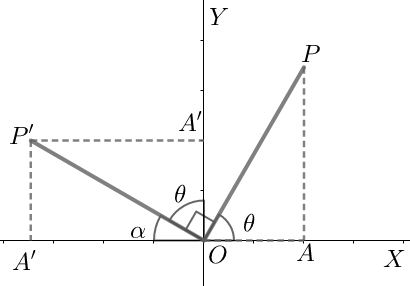
Note: We can also solve the problem in another way. We can take the help of graphical method. Now, $\sin \left( {{90}^{\circ }}+\theta \right)$ from the figure means \[\dfrac{A'P'}{OP'}\] which also equals the value $\dfrac{OA}{OP}$ since the triangles $\Delta OAP,\Delta OA'P'$ are congruent. $\dfrac{OA}{OP}$ would mean nothing but $\cos \theta $ . Hence, proved.