Question

Prove that “ In two concentric circles, a chord of the bigger circle, that touches the smaller circle, is bisected at the point of contact with the smaller circle”.

Answer 1

Hint: Concentric circles are those circles which have the same centre. If a line touches a circle, it means that the line is tangent to that circle. Use the property that the tangent and radius are perpendicular to each other at the point of contact. Use the fact that the perpendicular from the centre of a circle to the chord bisects the chord. Hence prove that the chord is bisected at the point of the contact.

Complete step-by-step solution -

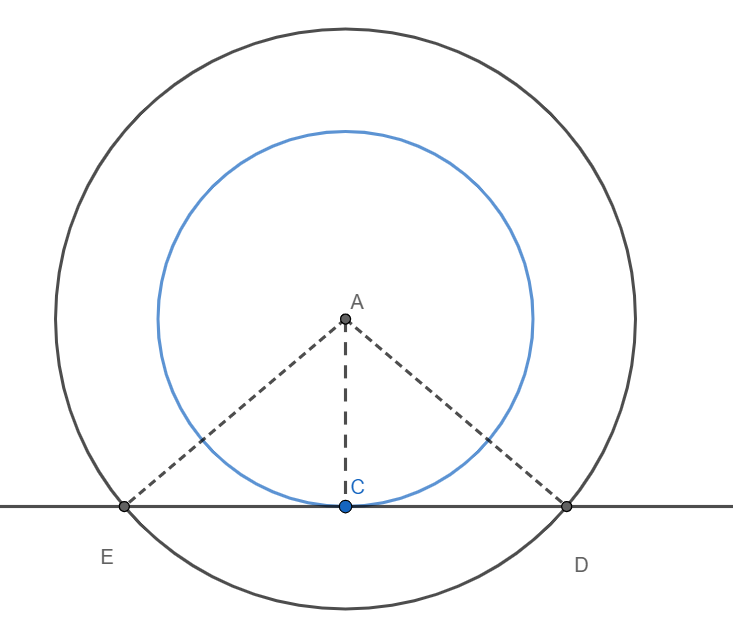
Given: Two concentric circles with the centre as A. ED is a chord of the larger circle which is tangent to the smaller circle.
To prove: C bisects ED, i.e. CD = EC
We have ED as a tangent to the circle with the smaller radius at the point of contact.
Since radius and the tangent are perpendicular to each other at the point of contact, we have $\text{AC}\bot \text{ED}$.
Hence AC is perpendicular from A on ED.
Now we have ED as a chord of the larger circle and AC is perpendicular from the centre to the chord.
Since perpendicular from the centre to the chord bisects the chord, we have AC bisects ED.
Hence C is the midpoint of ED and EC = CD.
Hence proved.

Note: In the above solution, we have used the property that perpendicular from the centre to the chord bisects the chord.
Proof:
Consider the triangles AEC and ADC.
We have AC = AC [Common side]
AE = ED (radii of the same circle)
$\angle \text{ACE=}\angle \text{ACD}$ each 90.
Hence we have the triangle AEC and ADC are congruent by RHS congruence criterion.
Hence EC = CD (corresponding parts of congruent triangles)