Question

Prove that if the diagonals of parallelogram are equal then it is a rectangle

Answer 1

Hint: We know that parallelogram is a Quadrilateral with all opposite sides equal and parallel. Now the rectangle is a Quadrilateral with all its angle equal and opposite sides equal and parallel. Hence we can say that a rectangle is a Parallelogram with all angles equal. Now the diagonal divides the Parallelogram in triangles we will prove that the two triangles are congruent. Using the property of congruent triangles we will prove the adjacent angles are equal. For opposite angles to be equal we can directly apply the property of Parallelogram which says opposite angles of parallelogram are equal.

Complete step-by-step answer:
Now let us start with considering a Parallelogram ABCD with diagonals AC and BD equal.

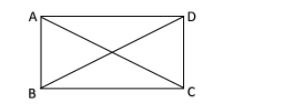
Now since ABCD is a parallelogram we know opposite sides are equal.
Now in triangle ADC and triangle BCD,
Hence we get AD = BC and AB = CD …….. (1)
Now we are given that the diagonals are equal
Hence, AC = BD …….. (2)
Hence from equation (1) and equation (2)
We have now triangle ADC and triangle BCD, AD = BC, AB = CD and AC = BD.
Hence from SSS test of congruence we can say that,
$\Delta ADC\cong \Delta BCD$
Now since the two triangles are Congruent corresponding angles are also congruent.
$\angle ADC=\angle BCD.................(3)$
Now since ABCD is a parallelogram opposite sides of this quadrilateral are equal, we get $\angle ADC=\angle ABC$ and $\angle BCD=\angle BAD$………….(4)
Hence from equation (3) and equation (4) we get
$\angle ADC=\angle ABC=\angle BCD=\angle BAD...............(5)$
Now we know that the interior angles of Quadrilateral add up to 360°.
Hence, $\angle ADC+\angle ABC+\angle BCD+\angle BAD={{360}^{\circ }}$.
Using equation (5) we now have
\[\begin{align}
  & \angle ADC+\angle ADC+\angle ADC+\angle ADC={{360}^{\circ }} \\
 & \Rightarrow 4\angle ADC={{360}^{\circ }} \\
 & \Rightarrow \angle ADC=\dfrac{360}{4}={{90}^{\circ }} \\
\end{align}\]
Now we have $\angle ADC={{90}^{\circ }}$
Again with the help of equation (5) we can say that
$\angle ADC=\angle ABC=\angle BCD=\angle BAD.={{90}^{\circ }}$
Hence, finally we have a Quadrilateral ABCD with opposite sides equal and parallel with all its angle equal to 90°.
Now the rectangle is a Quadrilateral with all its angles equal to 90° and opposite sides equal and parallel Hence, we can say that a parallelogram with its diagonal equal is a Rectangle.
Hence, Proved.

Note: Now we also have a property which says if any angle of Parallelogram is equal to 90° then the parallelogram is a Rectangle. Now after getting $\angle ADC=\angle BCD.$ in equation (3) we can use the fact that they are adjacent angles of Parallel sides and hence Complimentary. This will give us both angles to be equal to 90°. With this we can directly say that the Parallelogram is a rectangle.