Question

Prove that exponential function ${e^x}$ is an increasing function.

Answer 1

Hint:Here interval is not given so we will prove that ${e^x}$ is strictly increasing function in its own domain.

Complete step-by-step answer:
Let $f(x)$ is a function having ${D_f}$ as its domain. Range of exponential function is from \[(0,\infty )\].
$
f(x) = {e^x}\\
\therefore {D_f} \in R$

Now differentiating $f(x)$ with respect to $x$
${f^{'}}(x) = {e^{x}}$
Three cases arises $x > 0,x = 0,x < 0$
Case 1. When $x > 0$
${f^{'}}(x) = {e^{x}} = 1 + \dfrac{x}{{1!}} + \dfrac{{{x^2}}}{{2!}} + \dfrac{{{x^3}}}{{3!}} + .......$ Binomial expansion of exponential function ${e^{x}}$ > 0

Here we get that the overall function is greater than zero.
Case 2. When $x = 0$
$\therefore f'(x) = {e^x} = 1 > 0$ Putting value of $x = 0$ we get a function equal to 1 which again is greater than zero.
Case 3. When $x < 0$
$\therefore f'(x) = {e^x} = {e^{ - x}} = \dfrac{1}{{{e^x}}}$ = 1a positive quantity $ > 0$
Taking negative quantity and reciprocating it we will get positive quantity in denominator which is greater than zero.
In all the three cases we found out that $f'(x) = {e^x} > 0$
$\therefore $ The function ${e^x}$ is increasing.


Note: The word exponential has mathematical meaning which says extending in a natural way. It is a monotonically increasing function. A monotonous function is a function in which $x$ increases for all real values .The exponential function is one of the most important functions in mathematics somewhat lower than that of a linear function. Exponential functions provide simplest solutions to the dynamic systems. They can be related to a growth or decay of a process of a system over s period of time.
Alternative approach to this question is the Graphical method. In this we can see that function is increasing.
Putting $x = 0$, in function $y = {e^x}$ we will get $y = 1$ and by putting $x = 1$we will get $y = e$ which will be approximately equal to $2.718$

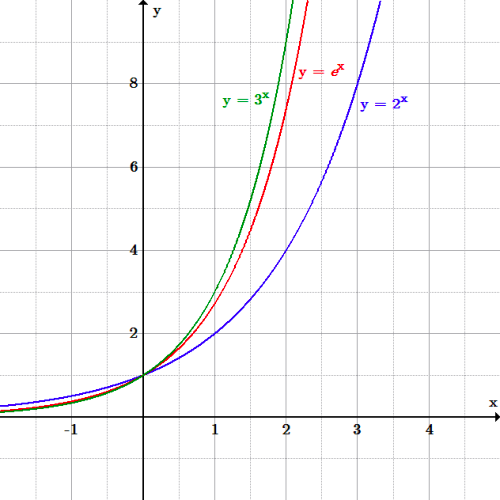
We can see that in the graph the function is increasing to infinity.