Question

Prove that $\csc \left( {{\csc }^{-1}}x \right)=x,x\in \left( -\infty ,-1 \right]\bigcup \left[ 1,\infty \right)$

Answer 1

Hint: Use the fact that if $y={{\csc }^{-1}}x$, then $x=\csc y$. Assume $y={{\csc }^{-1}}x$. Write $\csc \left( {{\csc }^{-1}}x \right)$ in terms of y and hence prove the above result.

Complete step-by-step answer:
Before dwelling into the proof of the above question, we must understand how ${{\csc }^{-1}}x$ is defined even when $\csc x$ is not one-one.
We know that cosecx is a periodic function.
Let us draw the graph of cosecx

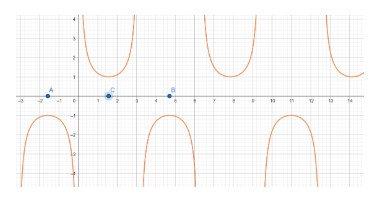
As is evident from the graph cosecx is a repeated chunk of the graph of cosecx within the interval $\left[ A,B \right]-\left\{ 0,\pi \right\}$ , and it attains all its possible values in the interval $\left[ A,C \right]-\left\{ 0 \right\}$, where $A=\dfrac{-\pi }{2},B=\dfrac{3\pi }{2}$ and $C=\dfrac{\pi }{2}$
Hence if we consider cosecx in the interval [A, C], we will lose no value attained by cosecx, and at the same time, cosecx will be one-one and onto.
Hence ${{\csc }^{-1}}x$ is defined over the Domain $\left( -\infty ,-1 \right]\bigcup \left[ 1,\infty \right)$, with codomain $\left[ \dfrac{-\pi }{2},\dfrac{\pi }{2} \right]-\left\{ 0 \right\}$ as in the Domain $\left[ \dfrac{-\pi }{2},\dfrac{\pi }{2} \right]-\left\{ 0 \right\}$, cosecx is one-one and ${{R}_{\csc x}}=\left( -\infty ,-1 \right]\bigcup \left[ 1,\infty \right)$.
Now since ${{\csc }^{-1}}x$ is the inverse of cosecx it satisfies the fact that if $y={{\csc }^{-1}}x$, then $\csc y=x$.
So let $y={{\csc }^{-1}}x$
Hence we have cosecy = x.
Now $\csc \left( {{\csc }^{-1}}x \right)=\csc y$
Hence we have $\csc \left( {{\csc }^{-1}}x \right)=x$.
Also as x is in the Domain of ${{\csc }^{-1}}x$, we have $x\in \left( -\infty ,-1 \right]\bigcup \left[ 1,\infty \right)$.
Hence $\csc \left( {{\csc }^{-1}}x \right)=x,x\in \left( -\infty ,-1 \right]\bigcup \left[ 1,\infty \right)$

Note: [1] The above-specified codomain for ${{\csc }^{-1}}x$ is called principal branch for ${{\csc }^{-1}}x$. We can select any branch as long as $\csc x$ is one-one and onto and Range $=\left( -\infty ,-1 \right]\bigcup \left[ 1,\infty \right)$. Like instead of $\left[ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right]-\left\{ 0 \right\}$, we can select the interval $\left[ \dfrac{\pi }{2},\dfrac{3\pi }{2} \right]-\left\{ \pi \right\}$. The proof will remain the same as above.