Question

Prove that $\cos \left( 36{}^\circ -A \right)\cos \left( 36{}^\circ +A \right)+\cos \left( 54{}^\circ +A \right)\cos \left( 54{}^\circ -A \right)=\cos 2A$ .

Answer 1

Hint: Try to simplify the left-hand side of the equation that we need to prove by using the property that $\cos \left( 90{}^\circ -\alpha \right)=\sin \alpha $ , $\cos \left( 90{}^\circ +\alpha \right)=-\sin \alpha $ , and other similar formulas. You will also need the formula $\cos A\cos B+\sin A\sin B=\cos \left( A-B \right)$ .
Complete step-by-step answer:
Before moving to the solution, let us discuss the periodicity of sine and cosine function, which we would be using in the solution. All the trigonometric ratios, including sine and cosine, are periodic functions. We can better understand this using the graph of sine and cosine.
First, let us start with the graph of sinx.

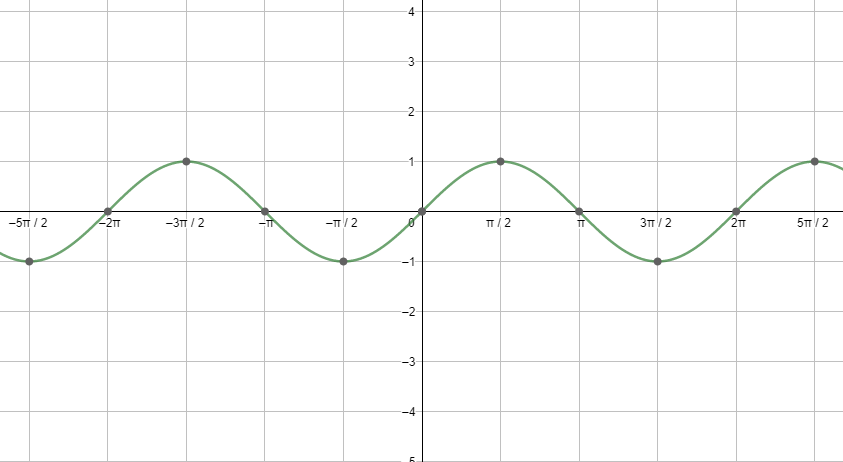
Next, let us see the graph of cosx.

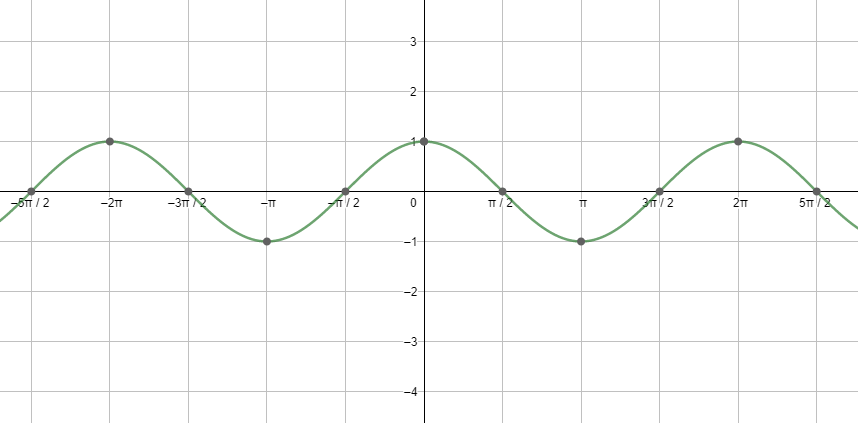
Looking at both the graphs, we can say that the graphs are repeating after a fixed period i.e. $2{{\pi }^{c}}$ . So, we can say that the fundamental period of the cosine function and the sine function is $2{{\pi }^{c}}=360{}^\circ $
We will now solve the left-hand side of the equation given in the question.
$\cos \left( 36{}^\circ -A \right)\cos \left( 36{}^\circ +A \right)+\cos \left( 54{}^\circ +A \right)\cos \left( 54{}^\circ -A \right)$
Now we know $\sin \left( 90{}^\circ -x \right)=\cos x$ . On putting these values in our expression, we get
$\cos \left( 36{}^\circ -A \right)\cos \left( 36{}^\circ +A \right)+\sin \left( 90{}^\circ -\left( 54{}^\circ +A \right) \right)\sin \left( 90{}^\circ -\left( 54{}^\circ -A \right) \right)$
$=\cos \left( 36{}^\circ -A \right)\cos \left( 36{}^\circ +A \right)+\sin \left( 36{}^\circ -A \right)\sin \left( 36{}^\circ +A \right)$
Now we know $\cos A\cos B+\sin A\sin B=\cos \left( A-B \right)$ . Therefore, our expression becomes:
$\cos \left( 36{}^\circ +A-\left( 36{}^\circ -A \right) \right)$
$=\cos 2A$
As we have shown that left-hand side of the equation given in the question is equal to right-hand side of the equation in the question we can say that we have proved that $\cos \left( 36{}^\circ -A \right)\cos \left( 36{}^\circ +A \right)+\cos \left( 54{}^\circ +A \right)\cos \left( 54{}^\circ -A \right)=\cos 2A$ .

Note: Be careful about the sign in the formula of cos(A-B). Also, be careful about the signs while opening the brackets, as the general mistake that a student can make is 1+x-(x-1)=1+x-x-1. Also, you need to remember the properties related to complementary angles and trigonometric ratios. Whenever you come across a question where you see the trigonometric ratios of non-standard angles, always try to eliminate the non-standard angles using trigonometric identities, as we did in the above question.