Question

Prove that \[\cos ({570^ \circ })\sin ({510^ \circ }) + \sin ( - {330^ \circ })\cos ( - {390^ \circ }) = 0\]

Answer 1

Hint: We break the angle values inside the bracket in such a way so we can relate to the quadrants in the plane and write the values for the question in a simpler way. Try to break the values as adding or subtracting from \[{360^ \circ },{180^ \circ }\]and relate to the quadrant diagram.
* We know the values of all trigonometric angles are positive in the first quadrant.
Values of only \[\sin \theta \] are positive in the second quadrant.
Values of only \[\tan \theta \] are positive in the third quadrant.
Values of only\[\cos \theta \] are positive in the fourth quadrant.

Complete step-by-step answer:
We solve for all the trigonometric terms separately.
For better understanding we draw the quadrant division

     

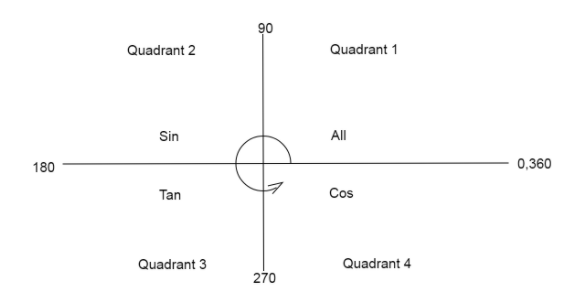
Firstly we solve for \[\cos ({570^ \circ })\]
We can write
\[\cos ({570^ \circ }) = \cos ({360^ \circ } + {210^ \circ })\]
Since \[{360^ \circ } + \] goes to the first quadrant where all trigonometric angles are positive
\[ \Rightarrow \cos ({360^ \circ } + {210^ \circ }) = \cos ({210^ \circ })\]
Now we can write
\[\cos ({210^ \circ }) = \cos ({180^ \circ } + {30^ \circ })\]
Since \[{180^ \circ } + \] goes to the third quadrant where all \[\tan \] angles are positive, so all \[\cos \] angles are negative.
 \[ \Rightarrow \cos ({180^ \circ } + {30^ \circ }) = - \cos ({30^ \circ }) = \dfrac{{ - \sqrt 3 }}{2}\]
So, \[\cos ({570^ \circ }) = \dfrac{{ - \sqrt 3 }}{2}\] … (1)
Now we solve for \[\sin ({510^ \circ })\]
We can write
\[\sin ({510^ \circ }) = \sin ({360^ \circ } + {150^ \circ })\]
Since \[{360^ \circ } + \] goes to the first quadrant where all trigonometric angles are positive
\[ \Rightarrow \sin ({360^ \circ } + {150^ \circ }) = \sin ({150^ \circ })\]
Now we can write
\[\sin ({150^ \circ }) = \sin ({180^ \circ } - {30^ \circ })\]
Since \[{180^ \circ } - \] goes to the second quadrant where all \[\sin \] angles are positive.
 \[ \Rightarrow \sin ({180^ \circ } - {30^ \circ }) = \sin ({30^ \circ }) = \dfrac{1}{2}\]
So, \[\sin ({510^ \circ }) = \dfrac{1}{2}\] … (2)
Now we solve for \[\sin ( - {330^ \circ })\]
Since, \[\sin \] is an odd function therefore, \[\sin ( - \theta ) = - \sin \theta \]
\[ \Rightarrow \sin ( - {330^ \circ }) = - \sin ({330^ \circ })\]
We can write
\[ - \sin ({330^ \circ }) = - \sin ({360^ \circ } - {30^ \circ })\]
Since \[{360^ \circ } - \] goes to the fourth quadrant where all \[\cos \] angles are only positive.
\[ \Rightarrow - \sin ({360^ \circ } - {30^ \circ }) = - \sin ( - {30^ \circ })\]
Since, \[\sin \] is an odd function therefore, \[\sin ( - \theta ) = - \sin \theta \]
\[ \Rightarrow - \sin ({360^ \circ } - {30^ \circ }) = \sin ({30^ \circ }) = \dfrac{1}{2}\]
So, \[\sin ({-330^ \circ }) = \dfrac{1}{2}\] … (3)
Now we solve for \[\cos ( - {390^ \circ })\]
Since, \[\cos \] is an even function therefore, \[\cos ( - \theta ) = \cos \theta \]
\[ \Rightarrow \cos ( - {390^ \circ }) = \cos ({390^ \circ })\]
We can write
\[\cos ({390^ \circ }) = \cos ({360^ \circ } + {30^ \circ })\]
Since \[{360^ \circ } + \] goes to the first quadrant where all trigonometric angles are positive
\[ \Rightarrow \cos ({360^ \circ } + {30^ \circ }) = \cos ({30^ \circ }) = \dfrac{{\sqrt 3 }}{2}\]
So, \[\cos ( - {390^ \circ }) = \dfrac{{\sqrt 3 }}{2}\] … (4)
Substitute values from equation (1), (2), (3) and (4) in the following equation
\[\cos ({570^ \circ })\sin ({510^ \circ }) + \sin ( - {330^ \circ })\cos ( - {390^ \circ }) = 0\]
\[
  \dfrac{{ - \sqrt 3 }}{2} \times \dfrac{1}{2} + \dfrac{1}{2} \times \dfrac{{\sqrt 3 }}{2} = 0 \\
  \dfrac{{ - \sqrt 3 }}{4} + \dfrac{{\sqrt 3 }}{4} = 0 \\
  0 = 0 \\
 \]
Therefore, LHS=RHS
Hence Proved

Note: Students can many times make mistakes when the angle between the brackets is negative, so always check first if the trigonometric function alone is an even or odd function. An odd function brings out the negative sign while an even function eradicates the negative sign.