Question

Prove that angles opposite to equal sides of an isosceles triangles are equal.

Answer 1

Hint: Construct an isosceles triangle with opposite sides equal. Altitude from the apex bisects the angle, dividing the triangles are equal. Thus the opposite angles will be equal.

Complete step-by-step answer:

Now let us consider the isosceles triangle ABC, which we have drawn.

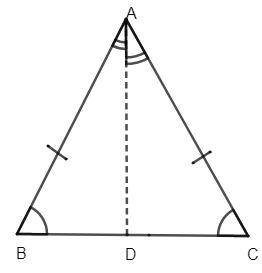
We know the basic properties of the isosceles triangle that are two sides of are congruent to each other. So let us consider from the figure that side AB and AC are congruent.
i.e. AB =AC.
We need to prove that \[\angle B\] is equal to \[\angle C\], \[\angle B=\angle C\].
Now let us draw AD perpendicular BC. The altitude from the apex of an isosceles triangle bisects the base into two equal parts and also bisects its apex angle into two equal parts.
Similarly, the altitude from the apex of an isosceles triangle divides the triangle into two congruent right angles triangles.
Thus from the given figure, let us consider \[\Delta BAD\] & \[\Delta CAD\].
We know that AB = AC.
\[\angle BAD=\angle CAD\] {altitude from apex of an isosceles triangle bisects the angle}
AD = AD, this is common for both triangles.
Thus we can say that \[\Delta BAD\] is equal to \[\Delta CAD\], by SAS congruent rule, where 2 sides and one angle of one triangle is equal to 2 sides and one angle of another triangle.
\[\therefore \Delta BAD\cong \Delta CAD\], by SAS congruence rule
Thus we can say that \[\angle ABD\] is equal to \[\angle ACD\], as both triangles are equal.
i.e. \[\angle ABD=\angle ACD\]
\[\Rightarrow \angle B=\angle C\]
Hence we proved that the angles opposite to equal sides are equal.
Note: An isosceles triangle is a polygon that consists of 2 equal sides, two equal angles, three edges, three vertices and the sum of internal angles of a triangle is equal to \[{{180}^{\circ }}\].