Question

Prove that a line drawn through the endpoint of a radius and perpendicular to it is a tangent to the circle.

Answer 1

Hint: First we will start by the definition of tangent and then we will give an example for the tangent. Then, we will draw a circle and take a point on the circle hence it will be a radius then we will make a line perpendicular to the line and take a point outside the line and proceed with the proof using the properties of lines.

Complete step-by-step solution
First, let’s define what a tangent is. In geometry, the tangent line or simply tangent to a plane curve at a given point is the straight line that "just touches" the curve at that point. The point where the tangent touches the curve is called the point of tangency.
For example, the tangent to $f\left( x \right)=\sin x$ looks as follows:

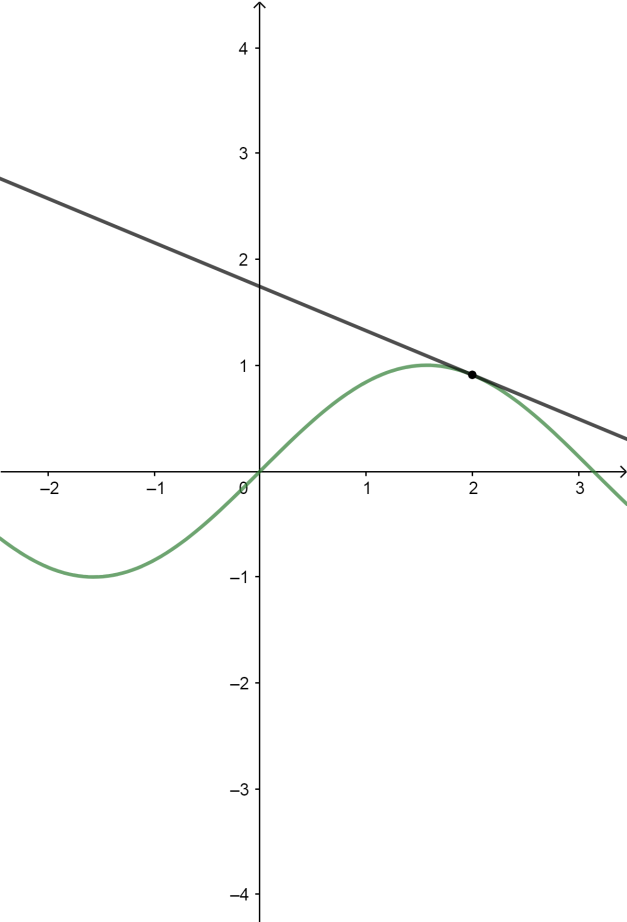
Now, we need to prove that a line drawn through the endpoint of a radius and perpendicular to it is a tangent to the circle.
Now, it is given that the radius $OP$ of a circle $C$ and a line $APB$ is perpendicular to $OP$,

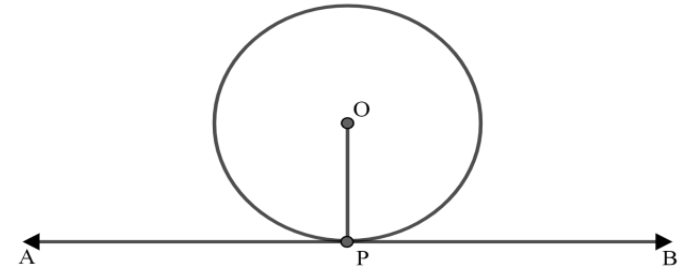
What we need to prove that \[AB\] is a tangent to the circle at the point $P$.
Now, we will take a point $Q$, different from $P$, on the line $AB$ as shown below:

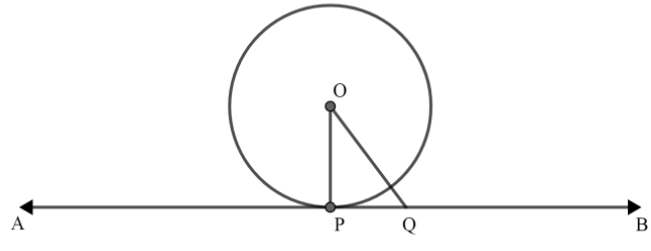
Now, it is given that radius is perpendicular to the given line which means: $OP\bot AB$, now we know that perpendicular on any line is the shortest, therefore: among all the line segments joining $O$ to a point on $AB$, $OP$ is the shortest.
That means, $OP< OQ\Rightarrow OQ> OP$, which implies that $Q$ lies outside the circle.
Thus, every point on $AB$, other than $P$, lies outside the circle. This shows that $AB$ meets the circle only at the point $P$.
Hence, $AB$ is a tangent to the circle at $P$.

Note: This is a basic theorem of the circle and the above theorem will provide us a method of constructing a tangent at a given point to a given circle. For this, we will draw a line through the given point perpendicular to the radius at the given point.