
Prove that:
$2{\sin ^2}\dfrac{\pi }{6} + {\operatorname{cosec} ^2}\dfrac{{7\pi }}{6}{\cos ^2}\dfrac{\pi }{3} = \dfrac{3}{2}$
Answer
590.7k+ views
Hint: Note that, \[{\text{since }}\dfrac{{7\pi }}{6}{\text{ is in third quadrant, therefore }}\operatorname{cosec} \dfrac{{7\pi }}{6}{\text{ is negative}}{\text{.}}\]
Then in the left hand side, substitute the values of \[\sin \dfrac{\pi }{6}\], \[\operatorname{cosec} \dfrac{{7\pi }}{6}\] and \[\cos \dfrac{\pi }{3}\].
And on solving we get the desired result.
Complete step-by-step answer:
Given to prove that $2{\sin ^2}\dfrac{\pi }{6} + {\operatorname{cosec} ^2}\dfrac{{7\pi }}{6}{\cos ^2}\dfrac{\pi }{3} = \dfrac{3}{2}$
Left hand side is given by,
\[2{\sin ^2}\dfrac{\pi }{6} + {\operatorname{cosec} ^2}\dfrac{{7\pi }}{6}{\cos ^2}\dfrac{\pi }{3}\]
The above expression can be written as,
\[ = 2{\sin ^2}\dfrac{\pi }{6} + {\operatorname{cosec} ^2}\left( {\pi + \dfrac{\pi }{6}} \right){\cos ^2}\dfrac{\pi }{3}\]
Since, \[\dfrac{{7\pi }}{6}\] is in the third quadrant, therefore \[\operatorname{cosec} \dfrac{{7\pi }}{6}{\text{ }}\] is negative,
\[ = 2{\sin ^2}\dfrac{\pi }{6} + {\left( { - \operatorname{cosec} \dfrac{\pi }{6}} \right)^2}{\cos ^2}\dfrac{\pi }{3}{\text{ }}\]
On simplification we get,
\[ = 2{\sin ^2}\dfrac{\pi }{6} + {\operatorname{cosec} ^2}\dfrac{\pi }{6}{\cos ^2}\dfrac{\pi }{3}\]
Using \[\sin \dfrac{\pi }{6} = \dfrac{1}{2},\cos \dfrac{\pi }{3} = \dfrac{1}{2},\cos ec\dfrac{\pi }{6} = 2\], we get,
\[ = 2 \times {\left( {\dfrac{1}{2}} \right)^2} + {\left( 2 \right)^2} \times {\left( {\dfrac{1}{2}} \right)^2}\]
On squaring we get,
\[ = \left( {2 \times \dfrac{1}{4}} \right) + \left( {4 \times \dfrac{1}{4}} \right)\]
On simplification we get,
\[ = \dfrac{1}{2} + 1\]
\[ = \dfrac{3}{2}\]
= Right hand side
Hence, $2{\sin ^2}\dfrac{\pi }{6} + {\operatorname{cosec} ^2}\dfrac{{7\pi }}{6}{\cos ^2}\dfrac{\pi }{3} = \dfrac{3}{2}$ (proved).
Note: Note the following important formulae:
1.$\cos x = \dfrac{1}{{\sec x}}$ , $\sin x = \dfrac{1}{{\cos ecx}}$ , $\tan x = \dfrac{1}{{\cot x}}$
2.${\sin ^2}x + {\cos ^2}x = 1$
3.\[{\sec ^2}x - {\tan ^2}x = 1\]
4.\[{\operatorname{cosec} ^2}x - {\cot ^2}x = 1\]
5.$\sin ( - x) = - \sin x$
6.$\cos ( - x) = \cos x$
7.$\tan ( - x) = - \tan x$
8.$\sin \left( {2n\pi \pm x} \right) = \sin x{\text{ , period 2}}\pi {\text{ or 3}}{60^ \circ }$
9.$\cos \left( {2n\pi \pm x} \right) = \cos x{\text{ , period 2}}\pi {\text{ or 3}}{60^ \circ }$
10.$\tan \left( {n\pi \pm x} \right) = \tan x{\text{ , period }}\pi {\text{ or 18}}{0^ \circ }$
Sign convention:
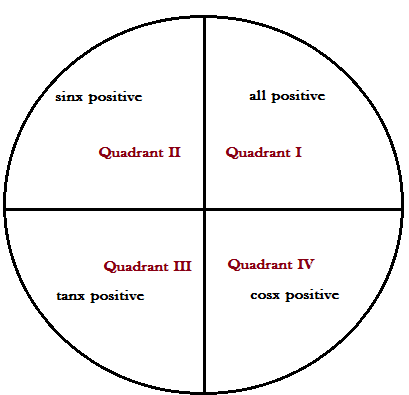
$\sin 2x = 2\sin x\cos x$
$\cos 2x = {\cos ^2}x - {\sin ^2}x = 1 - 2{\sin ^2}x = 2{\cos ^2}x - 1$
$\tan 2x = \dfrac{{2\tan x}}{{1 - {{\tan }^2}x}} = \dfrac{2}{{\cot x - \tan x}}$
Also, the trigonometric ratios of the standard angles are given by
Then in the left hand side, substitute the values of \[\sin \dfrac{\pi }{6}\], \[\operatorname{cosec} \dfrac{{7\pi }}{6}\] and \[\cos \dfrac{\pi }{3}\].
And on solving we get the desired result.
Complete step-by-step answer:
Given to prove that $2{\sin ^2}\dfrac{\pi }{6} + {\operatorname{cosec} ^2}\dfrac{{7\pi }}{6}{\cos ^2}\dfrac{\pi }{3} = \dfrac{3}{2}$
Left hand side is given by,
\[2{\sin ^2}\dfrac{\pi }{6} + {\operatorname{cosec} ^2}\dfrac{{7\pi }}{6}{\cos ^2}\dfrac{\pi }{3}\]
The above expression can be written as,
\[ = 2{\sin ^2}\dfrac{\pi }{6} + {\operatorname{cosec} ^2}\left( {\pi + \dfrac{\pi }{6}} \right){\cos ^2}\dfrac{\pi }{3}\]
Since, \[\dfrac{{7\pi }}{6}\] is in the third quadrant, therefore \[\operatorname{cosec} \dfrac{{7\pi }}{6}{\text{ }}\] is negative,
\[ = 2{\sin ^2}\dfrac{\pi }{6} + {\left( { - \operatorname{cosec} \dfrac{\pi }{6}} \right)^2}{\cos ^2}\dfrac{\pi }{3}{\text{ }}\]
On simplification we get,
\[ = 2{\sin ^2}\dfrac{\pi }{6} + {\operatorname{cosec} ^2}\dfrac{\pi }{6}{\cos ^2}\dfrac{\pi }{3}\]
Using \[\sin \dfrac{\pi }{6} = \dfrac{1}{2},\cos \dfrac{\pi }{3} = \dfrac{1}{2},\cos ec\dfrac{\pi }{6} = 2\], we get,
\[ = 2 \times {\left( {\dfrac{1}{2}} \right)^2} + {\left( 2 \right)^2} \times {\left( {\dfrac{1}{2}} \right)^2}\]
On squaring we get,
\[ = \left( {2 \times \dfrac{1}{4}} \right) + \left( {4 \times \dfrac{1}{4}} \right)\]
On simplification we get,
\[ = \dfrac{1}{2} + 1\]
\[ = \dfrac{3}{2}\]
= Right hand side
Hence, $2{\sin ^2}\dfrac{\pi }{6} + {\operatorname{cosec} ^2}\dfrac{{7\pi }}{6}{\cos ^2}\dfrac{\pi }{3} = \dfrac{3}{2}$ (proved).
Note: Note the following important formulae:
1.$\cos x = \dfrac{1}{{\sec x}}$ , $\sin x = \dfrac{1}{{\cos ecx}}$ , $\tan x = \dfrac{1}{{\cot x}}$
2.${\sin ^2}x + {\cos ^2}x = 1$
3.\[{\sec ^2}x - {\tan ^2}x = 1\]
4.\[{\operatorname{cosec} ^2}x - {\cot ^2}x = 1\]
5.$\sin ( - x) = - \sin x$
6.$\cos ( - x) = \cos x$
7.$\tan ( - x) = - \tan x$
8.$\sin \left( {2n\pi \pm x} \right) = \sin x{\text{ , period 2}}\pi {\text{ or 3}}{60^ \circ }$
9.$\cos \left( {2n\pi \pm x} \right) = \cos x{\text{ , period 2}}\pi {\text{ or 3}}{60^ \circ }$
10.$\tan \left( {n\pi \pm x} \right) = \tan x{\text{ , period }}\pi {\text{ or 18}}{0^ \circ }$
Sign convention:

$\sin 2x = 2\sin x\cos x$
$\cos 2x = {\cos ^2}x - {\sin ^2}x = 1 - 2{\sin ^2}x = 2{\cos ^2}x - 1$
$\tan 2x = \dfrac{{2\tan x}}{{1 - {{\tan }^2}x}} = \dfrac{2}{{\cot x - \tan x}}$
Also, the trigonometric ratios of the standard angles are given by
| \[0^\circ \] | \[30^\circ \] | \[45^\circ \] | \[60^\circ \] | \[90^\circ \] | |
| \[\operatorname{Sin} x\] | 0 | $\dfrac{1}{2}$ | $\dfrac{1}{{\sqrt 2 }}$ | $\dfrac{{\sqrt 3 }}{2}$ | 1 |
| \[\operatorname{Cos} x\] | 1 | $\dfrac{{\sqrt 3 }}{2}$ | $\dfrac{1}{{\sqrt 2 }}$ | $\dfrac{1}{2}$ | 0 |
| \[\operatorname{Tan} x\] | 0 | $\dfrac{1}{{\sqrt 3 }}$ | 1 | $\sqrt 3 $ | Undefined |
| \[Cotx\] | undefined | $\sqrt 3 $ | 1 | $\dfrac{1}{{\sqrt 3 }}$ | 0 |
| \[\cos ecx\] | undefined | 2 | $\sqrt 2 $ | $\dfrac{2}{{\sqrt 3 }}$ | 1 |
| \[\operatorname{Sec} x\] | 1 | $\dfrac{2}{{\sqrt 3 }}$ | $\sqrt 2 $ | 2 | Undefined |
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




