Question

How do you prove \[\cos \theta \sec \theta = 1\]?

Answer 1

Hint: Here, we will use the values of the trigonometric functions in a right-angled triangle and find the relationship between the given two trigonometric functions. Substituting that relationship in the LHS, we will be able to show that the left-hand side is equal to the right-hand side, thus, proving the given expression.

Formula Used:
 \[\sec \theta = \dfrac{1}{{\cos \theta }}\]

Complete step by step solution:
As we know, in a right angled triangle, whose base, perpendicular and the hypotenuse sides are \[B,P,H\] respectively,

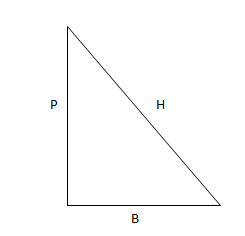
The measure of \[\cos \theta = \dfrac{B}{H}\]
And the measure of \[\sec \theta = \dfrac{H}{B}\]
Due to this, we can directly say that:
\[\sec \theta = \dfrac{1}{{\cos \theta }}\]
Hence, using this relation between cosine and secant trigonometric functions in the LHS, we get,
\[\cos \theta \sec \theta = \cos \theta \times \dfrac{1}{{\cos \theta }} = 1\]
By cancelling out the same trigonometric function from the numerator and the denominator we get
LHS \[ = \] RHS \[ = 1\]
Hence, since the LHS \[ = \] RHS

Therefore, \[\cos \theta \sec \theta = 1\]
Hence, proved.

Note:
In this question, we have used trigonometry. Trigonometry is a branch of mathematics that helps us to study the relationship between the sides and the angles of a triangle. In practical life, trigonometry is used by cartographers (to make maps). It is also used by the aviation and naval industries. In fact, trigonometry is even used by Astronomers to find the distance between two stars. Hence, it has an important role to play in everyday life. The three most common trigonometric functions are the tangent function, the sine, and the cosine function. In simple terms, they are written as ‘sin’, ‘cos’, and ‘tan’. Hence, trigonometry is not just a chapter to study, in fact, it is being used in everyday life.