Question

Projection of uniform circular motion on a diameter is
A. Simple harmonic motion.
B. Angular simple harmonic motion.
C. Both A and B.
D. None of these.

Answer 1

Hint:Simple harmonic motion or linear simple harmonic motion occurs when a particle moving along a straight line with acceleration whose direction is always towards a fixed point on the line and whose magnitude is proportional to the distance from the fixed point. Angular simple harmonic motion occurs when a body’s angular acceleration is proportional to its angular displacement from a fixed angular position and directed towards that position

Complete step by step answer:

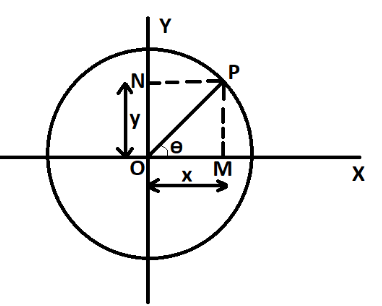
Let us consider a particle $P$ moving in a uniform circular motion about a point $O$ in the $XY$ plane as shown in the above figure.
Let $OP = r$
Splitting into horizontal and vertical component we can write $x$ and $y$ as
$x = rcos\theta $ and $y = r\sin \theta $ ……….. $\left( 1 \right)$
Since it is uniform circular motion then, $\theta $ increase in constant rate.
Therefore, $\theta = \omega t$ ……….. $\left( 2 \right)$
Substituting equation $\left( 2 \right)$ in equation $\left( 1 \right)$ we can write $x$ and $y$
$x = r\cos \omega t$ ………. $\left( 3 \right)$ and
$y = r\sin \omega t$ ……….. $\left( 4 \right)$
Differentiating equation $\left( 3 \right)$ two times that is on double differentiating with respect to $t$ , we get
$\dfrac{{{d^2}x}}{{d{t^2}}} = - {\omega ^2}r\cos \omega t = - {\omega ^2}x$ ……….. $\left( 5 \right)$
We know that acceleration is given by, $\dfrac{{{d^2}x}}{{d{t^2}}} = a$ ………… $\left( 6 \right)$
Where, $a$ is the acceleration along $x$ - axis
Comparing equation $\left( 5 \right)$ and $\left( 6 \right)$
$a = - {\omega ^2}x$ ………… $\left( 7 \right)$
We know that according to Newton’s second law,
$F = ma$ ………….. $\left( 8 \right)$
Substituting equation $\left( 7 \right)$ in equation$\left( 8 \right)$, we get
$F = - m{\omega ^2}x$
Let us assume, constant $K = m{\omega ^2}$, then $F = - Kx$
This force is directly proportional to the displacement, then the motion is said to be simple harmonic motion (S H M).Therefore projection of uniform circular motion on any diameter is linear simple harmonic motion (S H M).

Hence, the correct option is A.

Note: It should be noted that if the projection of uniform circular motion on a diameter is angular simple harmonic motion the force will be equal to \[\left( T \right) = - K\theta \] .Where, $T$ is the torque acting on the body